三角形二倍角公式大全(三角形二倍角关系)

导语：几何基本功一招搞定三角形二倍角问题 - 初中数学联赛几何100题之12

本专题我们精选了初中数学联赛几何类题目一共100题，非常适合日常的练习，拓展思维。如果你成功完成了这套题，那想必你的几何功力会极大提升，也非常欢迎各位题友参与讨论，分享你的精彩解法。

题目：已知：ABC 中，CBA = 2CAB ，CBA的角平分线 BD与CAB 的角平分线 AD 相交于点 D ，且 BC = AD .

求证：ACB = 60.

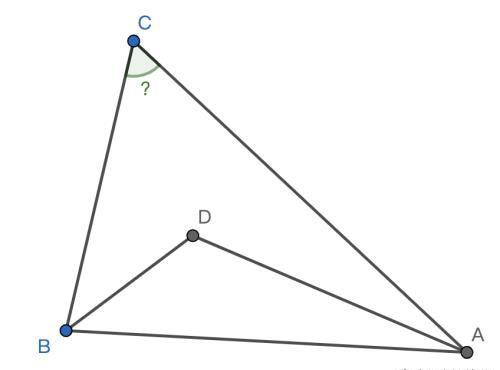
如果你想思考一下，可以暂停滚屏，思考1分钟后，再继续。

题目分析：

观察条件和结论的特征。

条件的一大特征是内心，难点在于如何把BC和AD这两条线段凑在一起，转化为有用的信息。常见的手段还是脱不了对称、平移、旋转。

解法一：利用对称作出三角形ABD的对称图形，从而将AD转化到与BC的同一三角形中。

令

作的角平分线交AC于E，易证

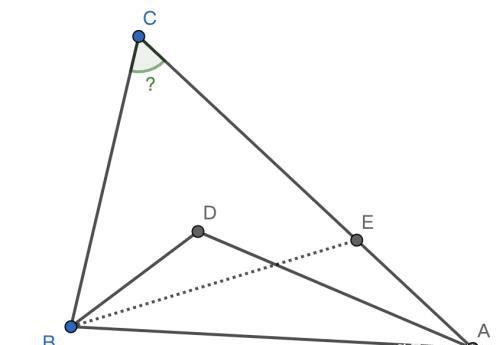
故BE=AD=BC

同时

所以三角形BCE为正三角形，，证毕

解法二：利用等腰梯形的对称性转移线段

作DE//AB交AC于E，因为

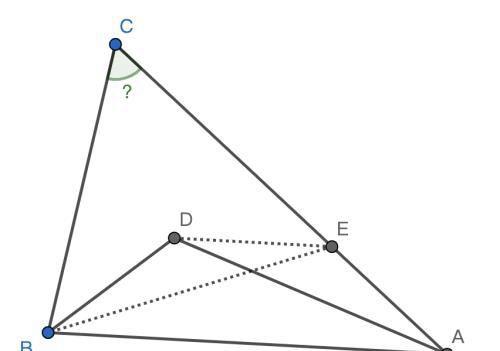
所以四边形DEAB为等腰梯形，从而BE=AD=BC

同样的，

所以三角形BCE为正三角形，

解法三：利用平行四边形平移AD

作AE//BD,BE//AD，得到平行四边形AEBD

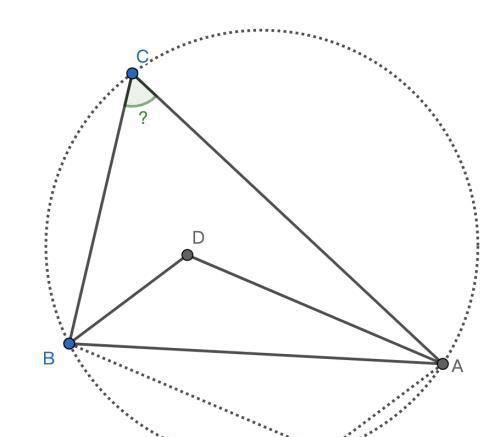
从而,且

加上BC=BE，∠AEB=∠ADB∠C

所以A,C,B,E四点共圆。

可得,即

补充：这里要注意的是这种四点共圆的证明方法，和直接使用张角相等、对角互补、外角等于内对圆幂定理逆定理、四点到定点距离相等这些方法都不同，值得展开一下。

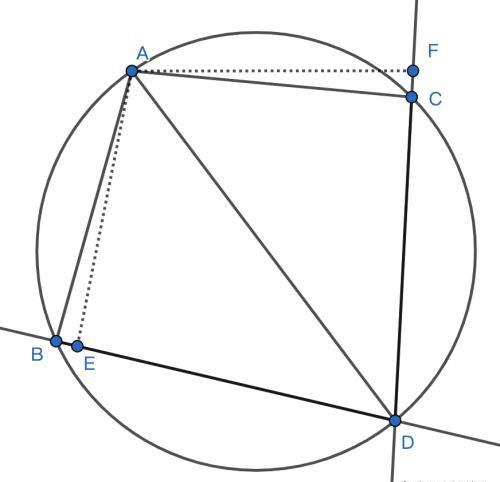
如上图，AB=AC,,问：A,B,C,D是否四点共圆？

过A分别作BD,CD的垂线，交BD,CD或其延长线于E,F点，分类讨论：

①如果∠ABD=∠ACD或者∠BAD=∠CAD， 则只有在时，

,结论成立。

如果时,结论不成立。

②如果∠ABD∠ACD，则此两角一为锐角一为钝角，E,F必有一点在ABCD内部，一点在ABCD外部。不妨设E点的线段BD上，F点的DC的延长线上。

易证

A,B,C,D四点共圆成立。

总结：二倍角加上平移、对称后的妙用。

你做对了吗？如果你有更好的方法，欢迎分享。

【卡拉数学】长期分享数学趣题、解题技巧，致力于数学科普和拓展数学思维，每日定更，觉得内容有兴趣的可以长期关注哦！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小滢创作整理编辑！