加法数字谜的题巧解的方法(加减法数字谜解题方法)

导语：［数字迷题之：加法解题技巧］加法数字迷基本常识及楼梯模型

在小学数学题中，有这样一种题型：叫做数字谜。跟猜谜语一样，给出一个加减乘除的计算式(一般是竖式计算)，把其中的一些数字用小方框□或者字母、汉字代替，让我们依据四则运算来推断□、字母或汉字所代表的数字。今天我们从最简单的加法数字迷开始，探寻其中的解题奥秘。

一、基本常识

①两个数字相加，最多进位是1

例：□+□=□□，则和的首位=1

②三个数字相加，最多进位是2

例：□+□+□=□□，则和的首位是1或2

③一个四位数减去一个三位数，结果是1，则这两个数为1000和999,同理，一个三位数减去一个两位数，结果是1，则这两个数为100和99，一个两位数减去一个一位数，结果是1，则这两个数为10和9。

例：

很明显，后面的计算是1000-999=1

④一个数A,若A+A=A,则A=0

例：

两个强相加还是强，可判断强=0

⑤两个数相加，某位数越加越少，说明有进位。

个位加4后变为3，肯定是有进位，因此，是9+4=13

二、楼梯模型

☞加法算式A+B=C

我们把A和B称为加数，C称为和。A、B、C的数字位数分别为a、b、c,则有如下性质

①一般情况下，c大于或等于a且c大于或等于b,若c比a和b都大，则数C的首位肯定是1。

②若a<b<c,即两个加数与和的位数均不同，呈现阶梯式分布，我们称A+B=C的竖式计算模型为楼梯模型。

举例：22+988=1010竖式计算形式为

形状像楼梯一样，呈阶梯状。

③楼梯模型性质

性质1 若a<b<c,则必有c=b+1,即和的位数比加数中位数最多的多一位，且和C的最高位是1

性质2：

❶若a<b<c,且b=a+1,即较大的加数比较小的加数多1位，则C的前2位是10，B的前1位是9

❷若a<b<c,且b=a+2,即较大的加数比较小的加数多2位，则C的前3位是100，B的前2位是99

❸若a<b<c,且b=a+3,即较大的加数比较小的加数多3位，则C的前4位是1000，B的前2位是999

❹若a<b<c,且b=a+n,即较大的加数比较小的加数多n位，则C的前n+1位是10…0(n个0)，B的前n位是99…9(n个9)

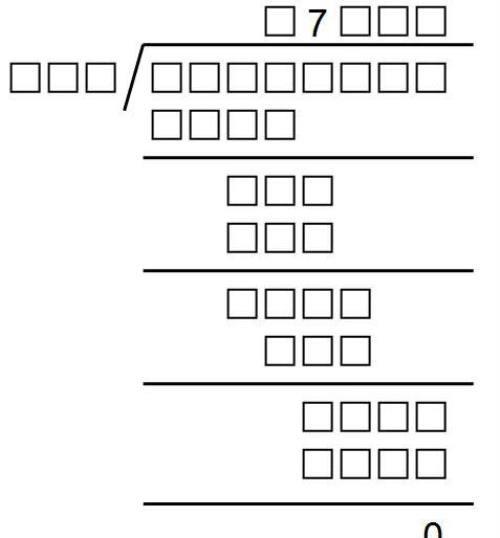
例题1：

可以判断和的前2位数字是10

较大的加数前1位数字是9

例2： 已知甲+乙=丙，且甲=2,

乙=□□□□，丙=□□□□□

则可以断定，乙=999□，丙=1000□

练习：

本文内容由小樊整理编辑！