求解一次函数解析式的方法(求一次函数解析式专题)

导语：初中数学：求解一次函数解析式只需掌握这两种方法（原理技巧）

网上各种初中求解一次函数解析式的说法很多，实际上根据初中知识只需并且也只能掌握两种方法，其他方法如两点法、斜截式、截距式等等都是高中的知识，中考根本涉及不到，完全没必要浪费时间和精力去理会。

初中数学课堂

一、待定系数法

原理方法：所谓待定系数法，是指先设待求直线方程或函数表达式（含有待定系数），再根据条件列出方程或方程组，求出待定系数，从而得到所求函数表达式的方法。

说明：此种方法不仅适合一次函数，还适合二次函数

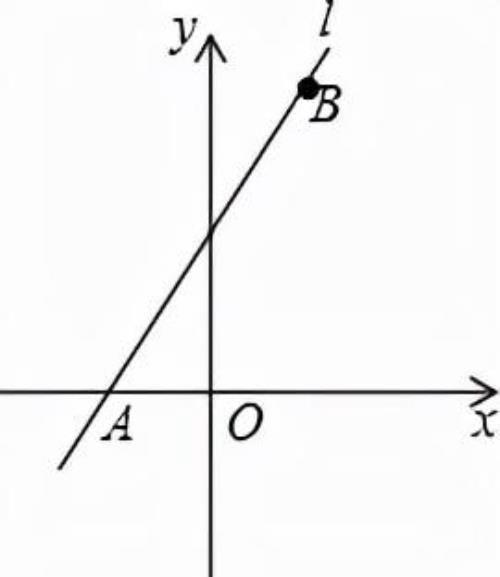
例1、如图，已知直线l1经过点A（﹣1，0）和点B（1，4），求直线l1的解析式；

解：设直线方程为y=kx＋b

∵该直线经过A、B两点

∴代入A（﹣1，0）和点B（1，4）得

k×(-1)+b=0; k+b=4

解得：k=2 , b=2

∴y = 2x+2

二、平移法

原理方法：一次函数无论是左右平移，还是上下平移，平移前后的两条直线始终保持平行，斜率不变，也即K值不会发生改变。

若平移前一次函数方程为y=kx+b, 平移后斜率不变，那么平移后函数可表示为 y=kx+c 。

当c=b时，两直线重合；当c≠b时，两直线平行。

例2、一次函数y=kx＋b（k≠0）的图象由直线y=3x向下平移得到，且过点A（1，2）．

（1）求一次函数的解析式；

（2）求直线y=kx＋b与x轴的交点B的坐标；

（3）设坐标原点为O，一条直线过点B，且与两条坐标轴围成的三角形的面积是1/2，这条直线与y轴交于点C，求直线AC对应的一次函数的解析式．

好的，今天就分享到这里，更多精彩等着你，敬请关注！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小曲创作整理编辑！