小学数学数图形的方法(小学数学数图形个数题目类型)
导语:小学数学常见的数图形问题,死记公式不如从图形规律入手解决
在小学二三年级,孩子们经常会遇到数图形个数问题,比如数线段的个数,数三角形的个数,数四边形的个数等问题,很多老师在教学的时候会总结出一套所谓的公式让孩子们去记,实际上这种方法对孩子的害处很大,一方面这种方法并不是普遍适用的,如果题目稍作调整和改变,这种方法就无所适从了,另一方面,简单的让孩子记公式会严重的限制孩子思维的发展,容易让他们养成固化的思维习惯,十分不利于孩子数学思维和解题能力的提高。
针对小学三年级大量出现的数图形个数问题,优博数学为您梳理了主要的几种数图形问题,供大家参考。同时,对于三年级学生来说,掌握常见的题型,并养成周周练习的习惯对于夯实基础,提高数学成绩尤为重要。今天,我系统的讲一下各个种类的数图形问题,以及相应的解决方法。
第一种:数线段个数问题。

如图,数出图中有多少个线段。这道题很多老师会让孩子在图中标记出数字,并将数字相加得出最终的结果,如下图所示。

最后的结果就是1+2+3+4=10。这个结果是正确的,但是这位老师并没有告诉同学们为什么要在线段上标记1,2,3,4,为什么这些数字要进行加法运算。事实上,如果图形发生了一点变化后,这个方法就无效了,比如:
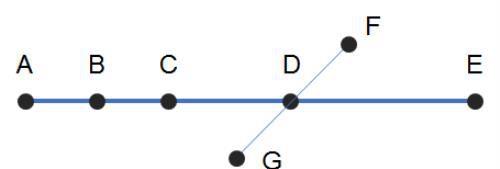
稍作变化,上面的方法就失灵了。因此说,死记硬背公式只能害了孩子。那么这道题应该怎样做呢?我们还是看一下原题的图形:

一种方法是从“小”线段数起,从单独的一个小线段开始,我们发现有AB,BC,CD,DE4条线段,再从两个部分构成的小线段看,有AC,BD,CE3条线段,再看由三个部分构成的线段,有AD,BE2条线段,再加上最大的那个线段,即AE,一共就有4+3+2+1=10条线段。

第二种方法是从左向右数,或者说是固定某一点开始依次数。首先我们固定A点,从A点出发,有AB,AC,AD,AE4条线段,再从B出发,有BC,BD,BE3条线段,从C出发有CD,CE2条线段,以及从D出发的DE这条线段。因此,一共有4+3+2+1=10条线段。需要注意的是,AB和BA是同一条线段,因此,从B、C、D开始数,都要向右数,而不再需要往左边再重复数。
很多家长可能会不屑于这种方法,认为这种方法太麻烦,而且没有公式算什么数学?实际上这种方法非常好,一方面,它鼓励孩子动手自己发现图形的规律,另一方面,这种方法正是应用到了重要的数学思维——分类的思想,将事物按照从小到大,或者从左到右的次序进行合理划分,通过这样的训练,会显著地提高孩子的思维能力。
第二种:数简单的长方形个数问题。
图中有几个长方形?

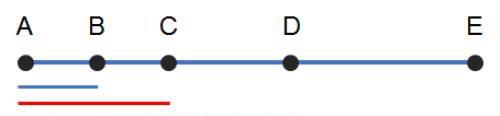
这是一道数长方形个数的问题,事实上,这道题和上一道题是一样的,我们把上一道题中的线变粗再和这道题比较一下。


所以,这道题也可以用两种方法解出:
①从小往大数,分别是单独的小长方形有AB,BC,CD,DE4个,两个长方形构成的长方形有AC,BD,CE3个,三个长方形构成的长方形有AD,BE2个,以及一个大的长方形AE。因此,一共有4+3+2+1=10个,下图给出了几种构造长方形的情形:



②从左往右数,先从A开始,依次有AB,AC,AD,AE4个,从B开始,有BC,BD,BE3个,从C开始,有CD,CE2个,以及DE,一共有4+3+2+1=10个长方形。
第三种:数角个数问题。
数一数图中有多少个角?
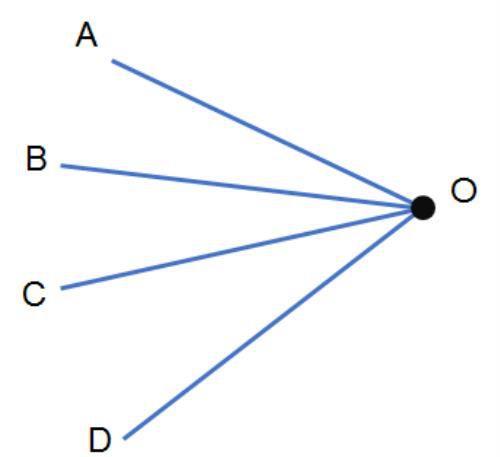
这类题也可以按照上面的方法,对图形进行分类分解,比如,可以按照从小往大数,先数相邻两条线夹成的角,有∠AOB,∠BOC, ∠COD3个,再数由两个角构成的角,有∠AOC, ∠BOD2个,再就是由3个角构成的最大的角∠ AOD,一共就有3+2+1=6个角。
当然,也可以顺次数,比如固定一条边OA,有∠ AOB, ∠ AOC, ∠ AOD3个角,再从OB出发,有∠BOC, ∠BOD2个角,再就是从OC出发的∠ COD,所以,一共有3+2+1=6个角。和数线段个数的方法一样,顺次数角的个数,也不需要往回再数,比如此例中从OB边出发,就不能再计算∠BOA了,因为∠BOA就是∠AOB。
第四种:数三角形个数问题。
数三角形个数是小学阶段最常见的数图形个数问题之一,简单的数三角形个数问题如下图所示:
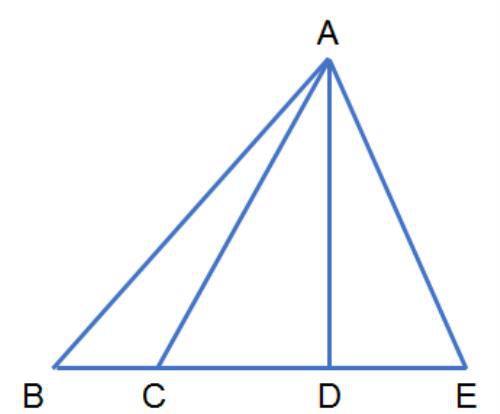
其实质还是数线段的个数,这道题和数线段,数简单长方形个数问题的方法是一样的,这里就不再赘述了。需要注意的是另一种稍微复杂的数三角形个数问题,如:
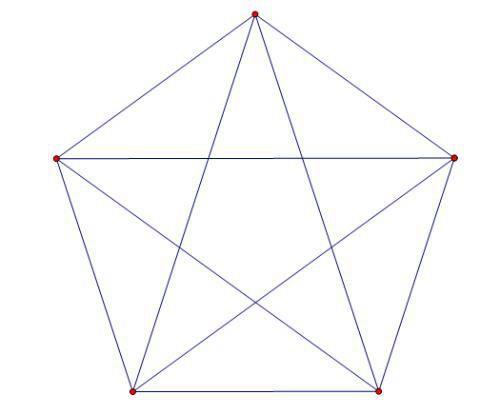
这类题需要仔细观察认真思考后才能保证答案的正确。首先,我们看单独形成的小三角形,一共有10个,如下图所示:
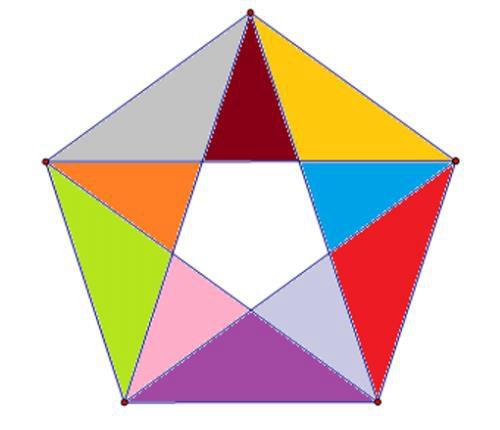
再数由两个部分组成的三角形,一共也是10个。

还有这五个:
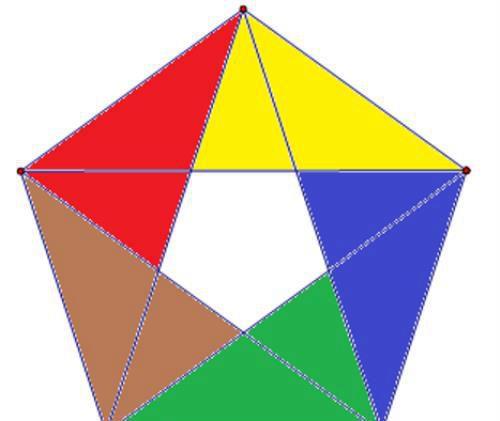
再来看由三个部分组成的三角形,也是10个,这种情形我们逐一示出:
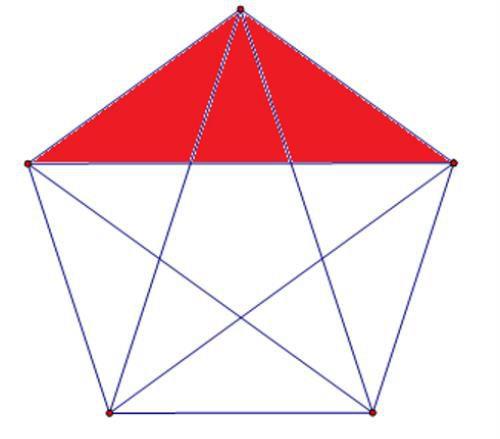
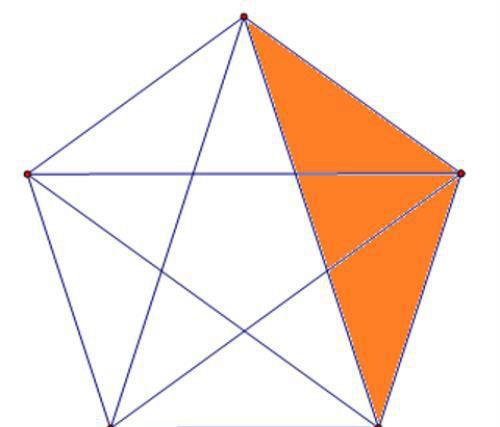

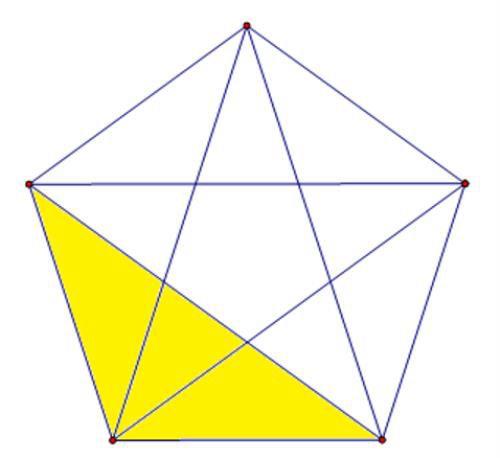
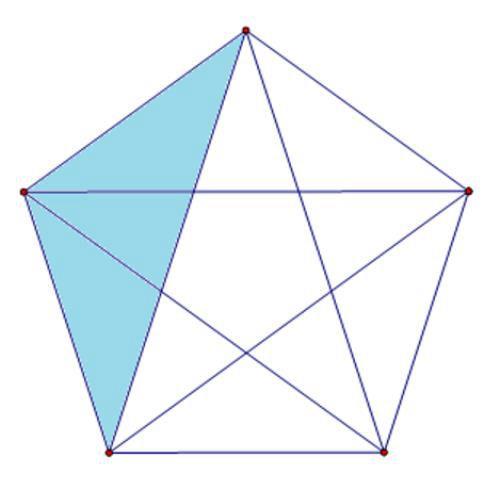
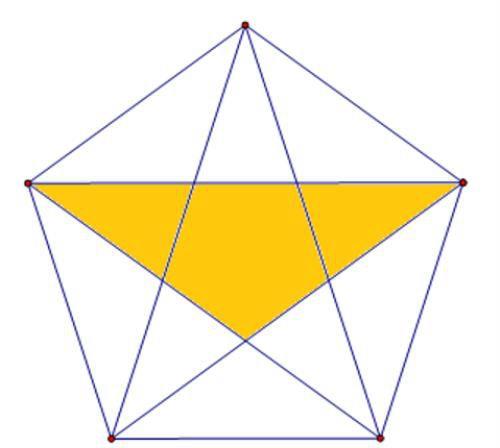
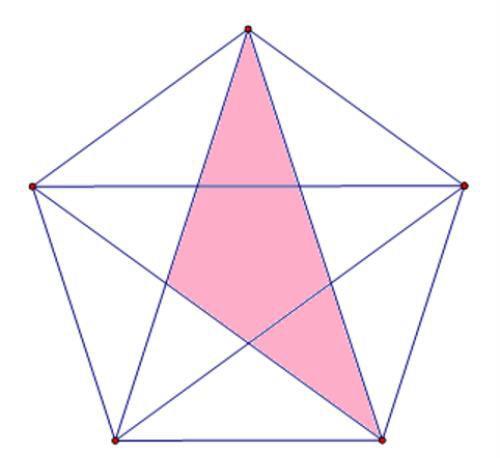

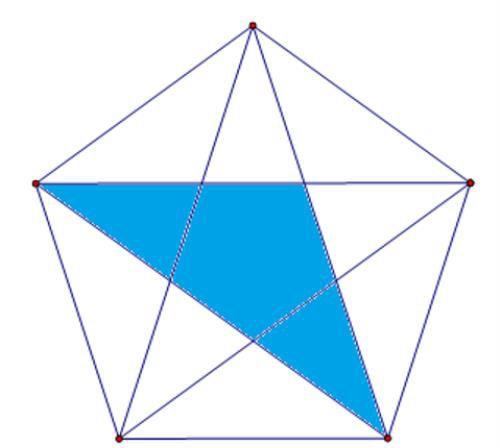

我们在数这类图形时,非常明显的一个规律就是图形之间呈现出一种旋转的关系,当然,我们也可以抓住某一个端点,依次变动这个点,这样数就能确保数出来的数字不多不少,既不会遗漏也不会重复。
最后,我们再数出由5个部分构成的三角形,有5种,参见下图。
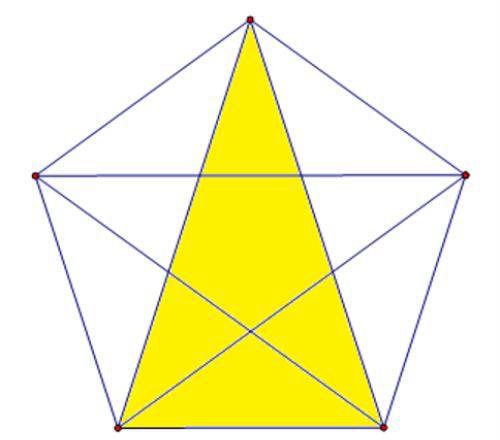
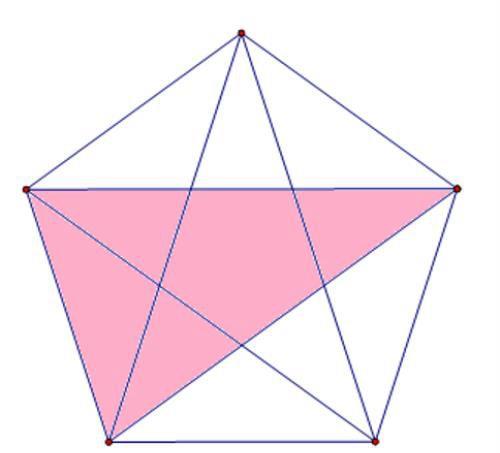
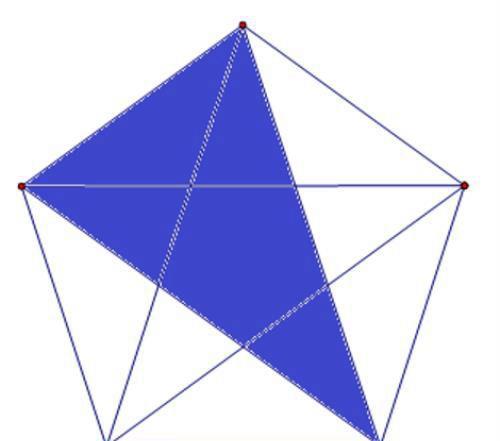

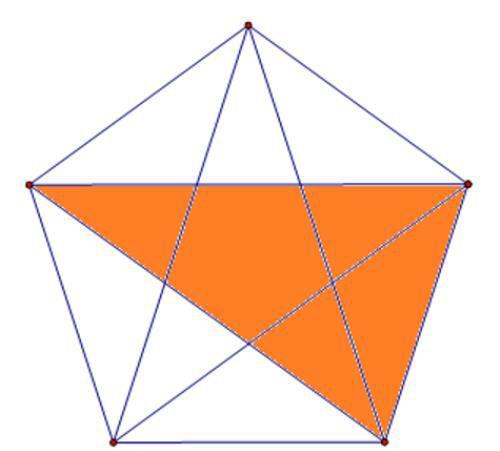
第五种:数复杂的长方形个数问题。
图中有多少个长方形?

这道题和上面提到的数长方形个数问题的一个主要的区别,就在于这道题有2行,因此,还不能简单的套用数线段图的方法,那么应该怎么做呢?
还是按照分类的思想对问题进行拆解,首先看由单独的一个图形构成的长方形,一共有6个,如图所示:

再来看由2个图形构成的长方形,有7个。


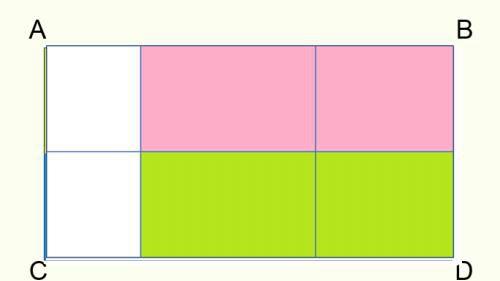
由3个图形构成的长方形有2个:

由4个图形构成的长方形有2个:


由6个图形构成的长方形有1个,即:

还有很多类型的数图形个数问题,不过大体上大同小异,上文列举的基本上已经涵盖了小学阶段主要的几种数图形个数问题。回顾这几道题目,我们总结出解此类题目的基本解题思路:
①先观察图形,发现图形的构成和类型;
②按照分类的思想,对图形按照一定的规则进行分类;
③依次数出各种图形的个数,相加求和即可。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑!