解决一类染色问题的通法有哪些(解决一类染色问题的通法原理)

导语：解决一类染色问题的通法

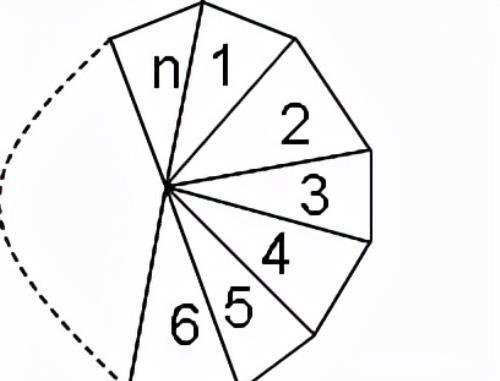
对于区域染色问题是高考中的一个难点，学生往往分类不清，选区域与选颜色相混造成错误，下面谈一下对于n个首尾相连的区域组成的多边形（如右图），若用k种颜色涂色，要求相邻区域不涂同种颜色，有多少种涂色方法的解法。

解：将n块的涂色方法种数设为an，显然当n=1时，a1=k，当n=2时，a2=k(k-1), 当n≥3时，对于n边形，若将1号色块与第n块剪开，则图形等价于：

若要求这条色带相邻两块不能同色，共有k种颜色，则应共有k乘以(k-1)的n-1次方种涂色方式，而an相当于要求1块和n块也涂不同颜色时的涂色方法数，下面我们看若当1与n颜色相同时，有多少种涂色方法，当1块与n块颜色相同时，相当于1块与n合并为一块时，相邻两块不同的涂色方法有a(n-1)种，所以可得下面的数列递推公式

本文内容由快快网络小面创作整理编辑！