求阴影面积割补法例题(求阴影部分面积小学)

导语：［小学1~6年级阴影面积三大求法］割补法、转化法、等差法

阴影面积三大求法

一、割补法

☞定义:有些非特殊特性不能直接求解，需通过割补后成为特殊图形易解；有些图形面积直接计算，计算量很大，耗时耗力还易做错，通过割补变为简单图形，计算量小，准确度大大提高。主要包括以下几种:

❶分割:把一个平面几何图形分割以后，各小块图形的面积(S1、S2……)之和，等于原图形的面积(S)。

☞公式:S=S1+S2+……

☞前提条件:S1、S2……都容易求解

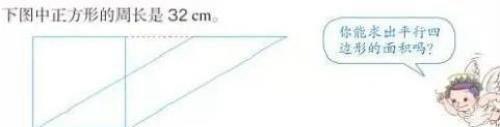
例子:如图所示，已知三个正方形的边长，求阴影面积。

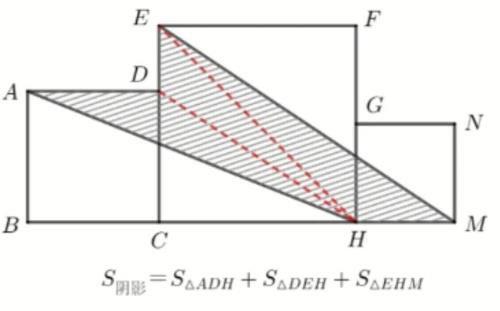
❷添补:有些图形没有可供分割的多余部分，又无法直接按面积公式求解，则需要用“补”的思路求解，通过添补一个图形(面积记为S1)后，整体组合成为特殊图形(面积容易求解的图形，面积记为S2)，再计算。

☞公式:S=S2-S1

☞前提条件:S1、S2都容易求解

例子:如图，已知BC和AD的长度，求四边形ABCD的面积

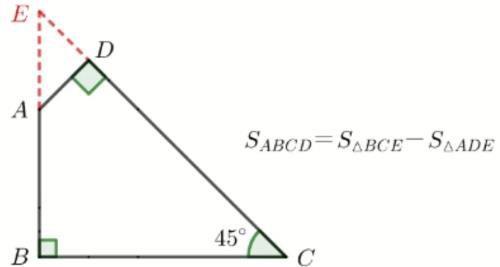
二、转化法

定义:通过等量代换、图形的变换(平移、旋转、割补)等方法得出所求的部分与另一部分(容易求)相等，因此通过直接求出另一部分而得到所求部分面积的的方法。

❶等量代换:找出与所求的未知图形(面积不容易求)面积相等的图形(面积容易求)。

S(未知)=S(容易求)

例题:

❷图形变换:通过图形的变换(平移、旋转、割补)等方法得出所求的部分与另一部分(容易求)相等。

S(未知)=S变换后(容易求)

例题:

三、等差法

定义:两个图形的面积之差，等于两个图形分别加上或者减去同一个图形的面积后之差。即:S1-S2=(S1+S)-(S2+S)=(S1-S)-(S2-S)

★此方法用于两个图形有部分重叠的情况。

例题:

如图所示，两个平行四边形ABCD和EFGH(底都是9厘米，高分别为6厘米、5厘米)存在部分重叠，扣除重叠部分后，两个平行四边形剩余部分面积分别为S1、S2,求S1-S2=？

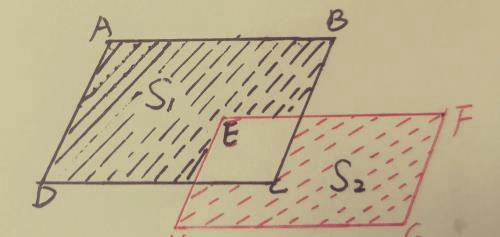
解:设重叠部分面积为S3,我们发现S1+S3与S2+S3分别是两个平行四边形ABCD和EFGH的面积，于是我们将所求S1-S2=？转化为

S1-S2=(S1+S3)-(S2+S3)=9×6-9×5=9(平方厘米)

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小熊创作整理编辑！