做这道题怎么做(做一道题会一类题是什么意思)

导语：做这样的题，就能“做一道题，会一类题”

做经典题，就能达到的目的。

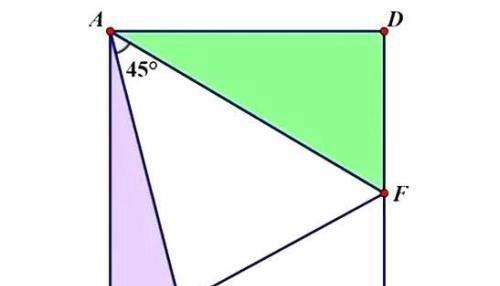
半角模型

【半角模型】在初中几何中占据重要地位，这一知识在解决一些有难度的几何题中应用广泛。下面我们就通过一道经典题来分析一下半角模型的应用。

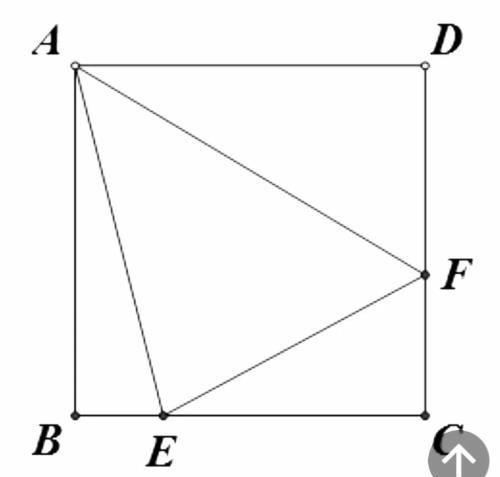
经典题图

一、【半角模型】经典题：

如图，在正方形 ABCD 中，点E、F分别在BC、CD上，∠EAF =45°，求证： EF = BE + DF .

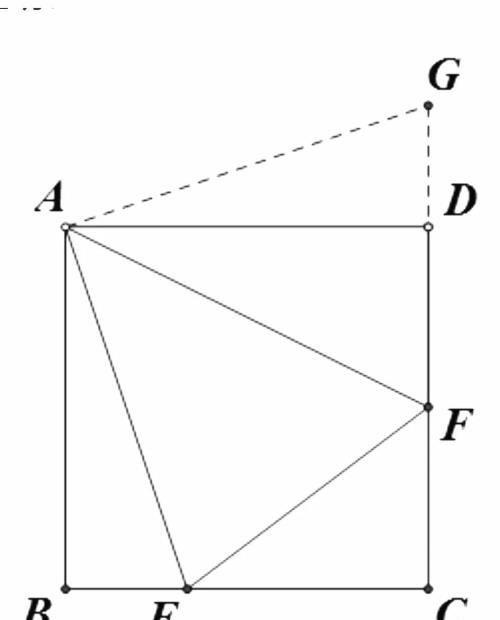
证明：EF=BE+DF

证明：

∵四边形 ABCD 是正方形，∴AB=AD且∠ABE+∠ADF =180°.

将△ABE 绕点 A 逆时针旋转90°，得到△ ADG ，此时点 C 、 D 、 G 三点共线．

∴∠BAE=∠DAG，AE=AG

∵∠EAF =45°

∴∠BAE+∠DAF=∠DAG+ ∠DAF=∠GAF= 45°.

∴∠EAF =∠GAF .

又∵AF = AF .

∴△ EAF ≌△ GAF .

∴EF=GF=DF+DG= DF+BE .

二、【题目应用】1：

如图，在正方形 ABCD 中，点E,F分别在边BC , CD上，∠DAE=20°，∠AFB=65°．求∠α=？

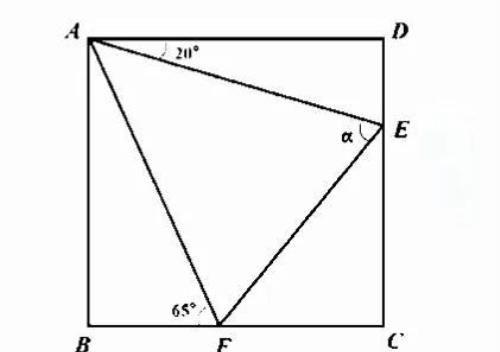
求∠α=70°

解：∵∠AFB=65°，∴∠BAF=25°.

∴∠EAF=90°-（25°+20°）=45°.

根据【半角模型】可证出∠AFB=∠AFE=65°，∠AED=∠AEF=∠α

∠AED=90°-20°=70°

∴∠α=70°.

【题目应用】2:

如图，在正方形 ABCD 中，点 E , F 分别在边BC , CD ，∠EAF =45°. BE =4cm，DF=6cm，求正方形的边长．

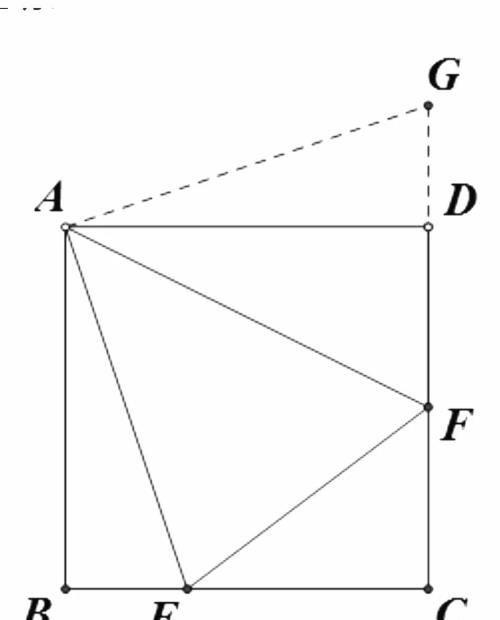
求正方形边长=12

解：根据【半角模型】得出的结论△AEF≌△AGF，

可知 EF = BE + DF =10.

设正方形的边长为 a，那么 CE = a-4， CF = a-6.

在Rt△CEF中，根据勾股定理得，CE²+ CF²= EF²,

即(a-4)²+(a-6)²=10²，解得，a =12. 所以正方形的边长为12cm。

【半角模型】其它可以证明的结论

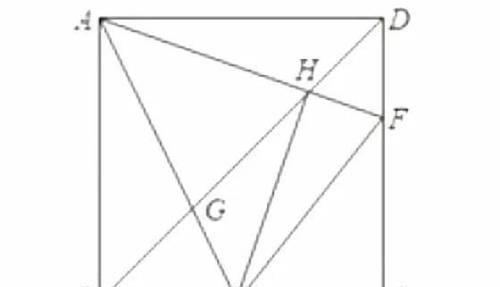
三、【半角模型】其它可以证明的结论：

（1）AE平分∠BEF，AF平分∠EFD.

（2）过点A作AK⊥EF，垂足为K，AK=AB.

（3）AH⊥EH.

（4）BG²+HD²=GH².

（5）△AGH∽△DFH.

（6）2AB=EF+EC+FC.

… …

四、【半角模型】：顾名思义，简单说就是一个角的度数是另一个角的一半。那么半角模型的几何题一般需要哪些条件呢？

（1）共顶点角存在半角。（2）角的两边两等。（3）对角互补。这三个条件缺一不可，为什么？因为，半角模型一般需要做旋转。因为解决半角模型的基本方法，就是做旋转，旋转得到另一个半角。（当然，也有通过截长或者补短，这只是辅助线的描述方式不一样，本质上还是在做旋转。)

我们知道这类中考题型，需要判断哪些结论是正确的，或者哪个结论不成立的？是很费时间和脑力的，还容易出错。但是，只要我们熟练了半角模型的一些常见结论，这些题也就“迎刃而解”了。

比如下面这道中考真题1，如果熟练掌握结论的话，立刻就知道选③，但不熟练半角模型，确实有点难，也许还没有时间去解题。所以解压轴题，也是有方法、有规律可以遵循的。

中考真题1

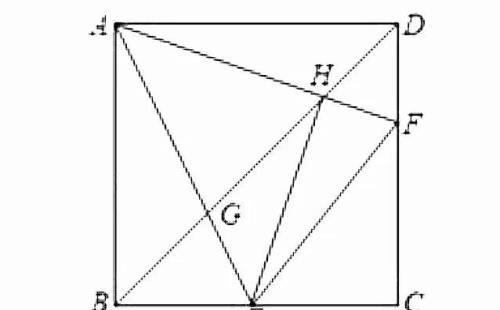
五、【中考真题】1：

如图，正方形 ABCD 中，点 E , F 分别为边BC , CD上的点，连接AE , AF ，与对角线BD分别交于点G , H ，连接EH，若∠EAF =45°，则下列判断错误的是（ ）。

① . BE + DF = EF.

②. BG²+ HD²= GH².

③ . E , F 分别为边 BC , CD 的中点.

④ . AH⊥EH.

中考真题2

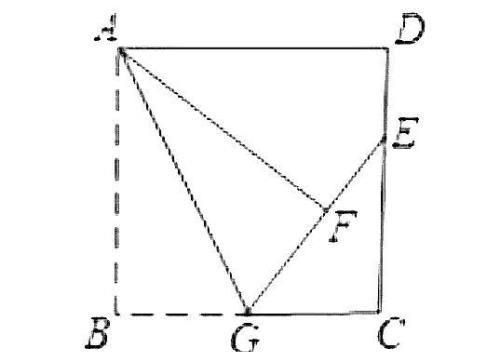
【中考真题】2：

如图，正方形 ABCD 中， AB=6cm, G 是 BC 的中点。将△ ABG 沿 AG 对折至△ AFG ，延长 GF 交 DC 于点 E ，则 DE 的长是（ ）。

①1cm ② 1.5 cm ③ 2cm ④ 2.5cm。

六、【半角模型】往往能把看似缺少已知条件或看似没有关联的已知条件整合为必要的解题条件，能使解题思路豁然开朗。做经典题要融会贯通、举一反三，就能达到的目的。

【半角模型】在等腰直角三角形、等边三角形、矩形等题型中的应用，我们下篇一起学习。

我们都可以迷上数学。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小里创作整理编辑！