无穷级数有关于求和的公式(求无穷级数的和例题)

导语：一道高中题-关于无穷级数和的计算

一道高中题-关于无穷级数和的计算

求下列无穷级数的和， 已知无穷级数是：

，

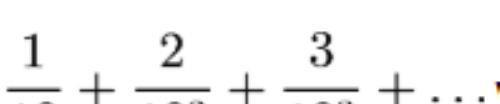
其第n项是：

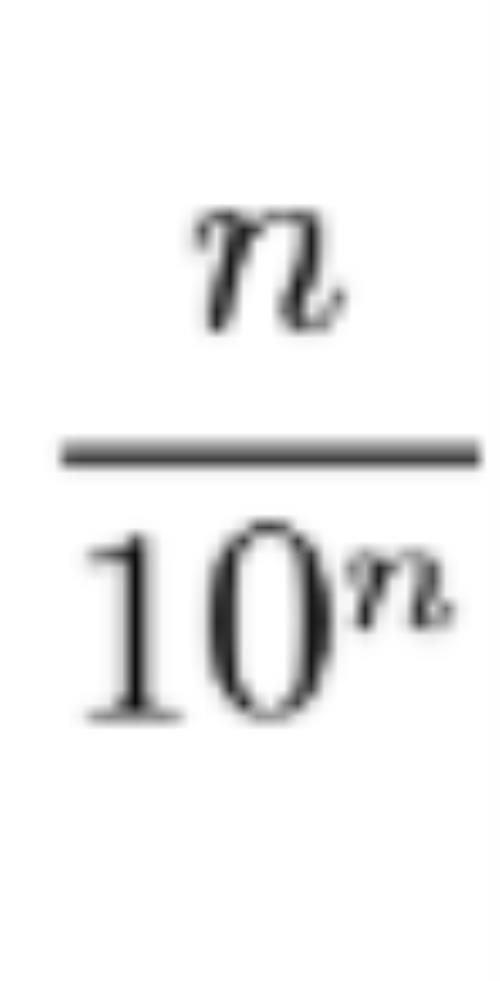
解法1：我们知道当n趋向无穷大的时候，

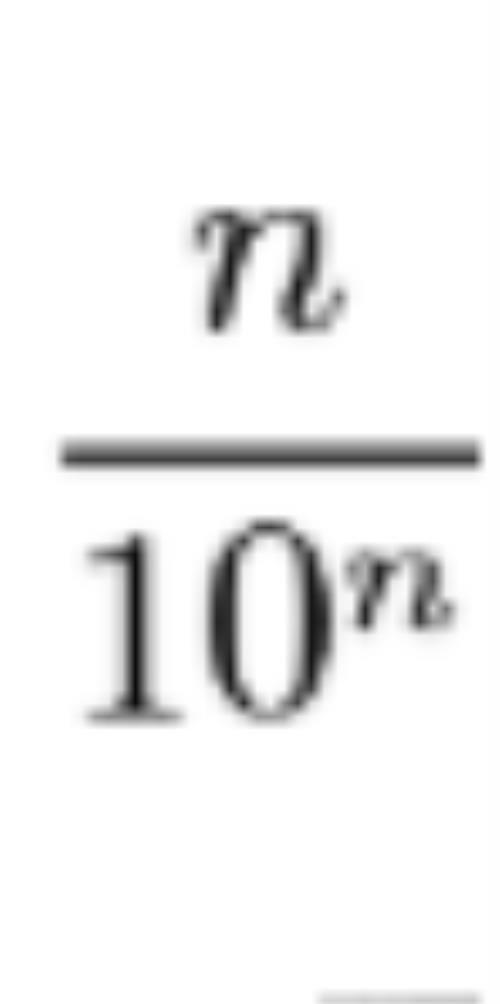
的值是趋于零的，因为分母是比分子更高级的无穷大。

所以整个数列的和在n趋近无穷大的时候是收敛的，因此有极限的值。

所给的数列之和可以写成：

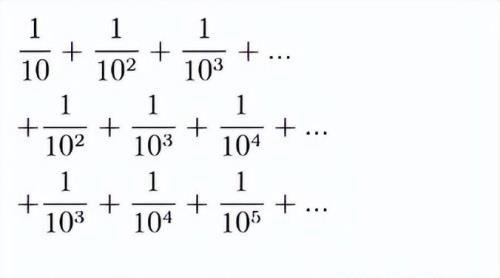
可以看出每一行的数理都是一个无穷的收敛的的等比数列，

因此和为：

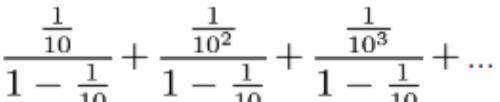
因为有公共的分母， 提出后， 分子也是一个无穷的收敛的等比数列

因此结果是：

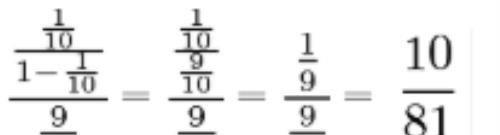
解法2：

设

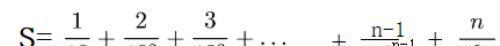
那么：

两边同时乘以1/10之和有：

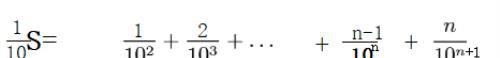
前式减去后式有：

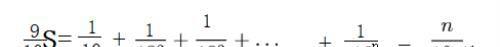
对于有限项的右侧前n项为等比数列， 若趋近无穷大，最后一项趋于零， 而等边数列的极限为(1/10)/(1-1/10)=1/9,

因此极限之和为（1/9）/(9/10)=10/81

总结：关于等比数列的公比q<1 的时候， 等比数列的和在n趋于无穷大的时候，是有极限的，其极限值为a/(1-q), a是首项。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小面创作整理编辑！