为什么考卷中总能看到它的答案(为什么试卷)

导语：为什么考卷中总能看到它？

此题为五年级数学下册必考题，主要考查学生的空间想象力由“平面图形”到“立体图形”的转化，以及解决实际生活问题的基本技能，检测了“平面图形”的边长、面积和“立体图形”的棱长、表面积、体积多个知识点理解和掌握情况。

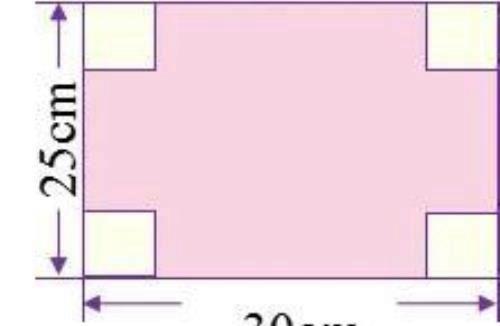
一块长方形铁皮(如右图)，从四个角各切掉一个边长为5 cm的正方形，然后做成盒子。这个盒子用了多少铁皮？它的容积有多少？

方法一

思路引导：求这个盒子用了多少铁皮，就是求所用铁皮的面积，可用长方形铁皮的面积减去切掉的4个正方形的面积；求容积可以求出做成的盒子的长、宽、高，再用长方体的体积公式进行计算。

规范解答： 表面积: 30×25-5×5×4=650(cm²)

容积:(30-5×2)×(25-5×2)×5=1500(cm³)

答: 这个盒子用了650 cm²铁皮，它的容积有1500 cm³。

方法二

思路引导：求这个盒子用了多少铁皮，就是求所用无盖盒子的表面积，可以先求出做成的盒子的长、宽、高，再根据长方体表面积的计算方法去求；求容积可以直接用长方体的体积公式进行计算。

规范解答：

长: 30-5×2 =20(cm) 宽: 25-5×2=15(cm)

表面积:

20×15+20×5×2+15×5×2=650(cm²)

容积: 20×15×5=1500(cm³)

答: 这个盒子用了650 cm²铁皮，它的容积有1500 cm³。

点评：解决本题关键是找出长方体的长、宽、高和原来长方形的长和宽之间的关系，求出长、宽、高即可解决问题。在孩子空间想象力差，疑惑不解的情况下，可以利用直观画图，动手实践等方法让孩子在画一画、剪一剪、折一折，比一比等活动中，充分感知长方体的长、宽、高和原来长方形的长和宽之间的关系，从而找到长方体的长、宽和高。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！