这道双曲线填空题有点难(这道双曲线填空题有点难怎么办)

导语：这道双曲线填空题有点难

题：如图，点A是双曲线y=-√2/x上一个动点，点A关于原点的对称点为B，△ABC为等腰直角三角形，∠C=90°，AC交x轴于点D，如果BD恰好平分∠ABC，则点C的坐标是 。

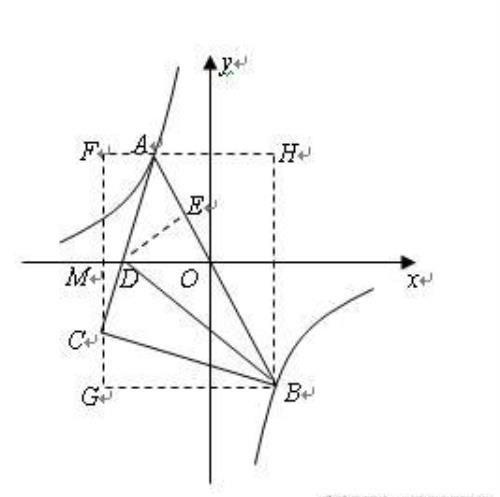
分析与解：在没有确定用什么方法求点C坐标时，首先注意到根据已知条件，点A在双曲线上，点B关于原点对称点是B，而双曲线是中心对称图形，所以点B也在双曲线上。其次，注意△ABC为等腰直角三角形，BD平分∠ABC，想到角平分线上的点到角两边距离相等，过点D作DE⊥AB于E，则DC=DE，△ADE是等腰直角三角形，

所以CD/AD=DE/AD=1/√2。

设点C的坐标为(x，y)，点A的坐标为(a，-√2/a)，

则点B的坐标为(-a，√2/a)，

注意到△ABC三个顶点A、B、C坐标的关联性，分别过A、B、C作坐标轴的平行线，围成一个矩形BGFH，则点G、F的坐标分别是：

G(x，√2/a)，F(x，-√2/a)，

所以CF=-√2/a-y，BG=-a-x，AF=a-x，CG=y-√2/a，

由∠C=90°，AC=BC易知：△ACF≌△CBG，

所以CF=BG，AF=CG。

所以-√2/a-y=-a-x，x-y=-a+√2/a……（1）

a-x=y-√2/a，x+y=a+√2/a……………（2）

（1）+（2），得2x=2√2/a，x=√2/a；

（2）-（1），得2y=2a，y=a。

设FG交x轴于M，则CM=-y=-a，MF=-√2/a，

因为DM∥AF，所以CM/MF=CD/AD，

所以-a/(-√2/a)=1/√2，整理，得a^2=1，

因为a<0，所以a=-1。

所以x=-√2，y=-1，

所以点C的坐标为(-√2，-1).

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小璎创作整理编辑！