一道圆的切线中考题写出你的简明的解法是什么(圆的切线题怎么做)

导语：一道圆的切线中考题，写出你的最简明的解法

做任何事都有方法，学习，解题也是如此。我们学生，有的没有熟记基础知识(需要多记);有的即使对基础知识有所掌握，但缺少对题中条件的深入，深入分析，不会联系相关的知识(需要多练);有的不能掌控所有的条件，分析一个，忘了另一个，条件之间不能互相融合，导至做题困难，虽然刻苦用功，但收效不大。下面以一道中档考题，给同学们分析一下，抛砖引玉，以期同学们有所收获。

【题目呈现】

如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E.

(1)求证∠A=∠ADE;

(2)若AD=16，DE=10，求BC的长.

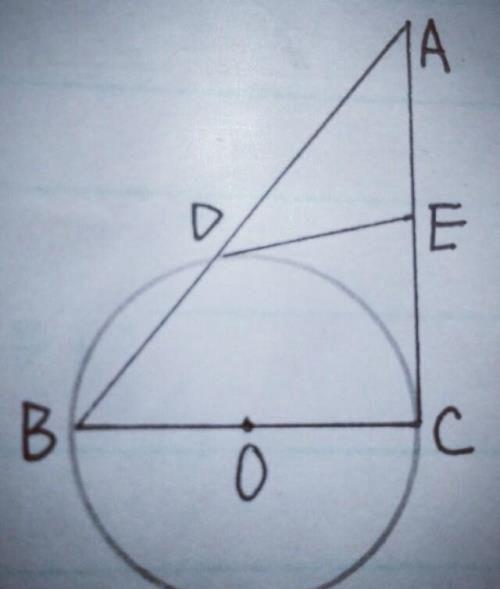
【分析】(1)，题中DE是⊙O的切线，想到连DO，则∠ODE=90°，则∠ADE+∠BDO=90°，而在Rt△ABC中，∠C=90°，∴∠A+∠B=90°，又∠B=∠BDO，∴∠A=∠ADE.如图

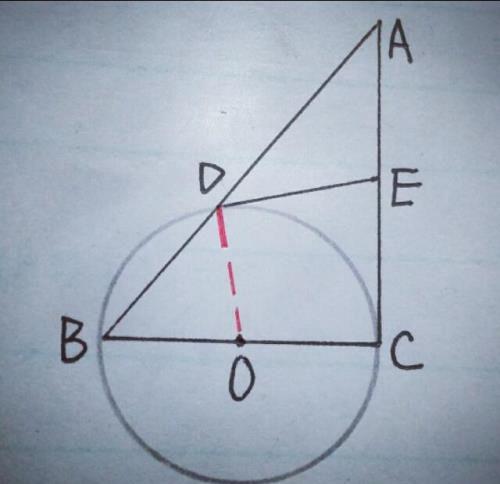
再看，∵BC是直径，∴连接DC，如图

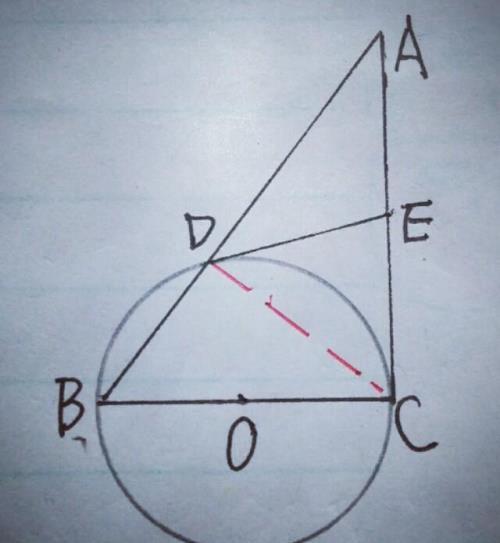
则，∠BDC=∠CDA=90°，而DE是⊙O的切线，又可证AC是⊙O的切线，∴DE=CE，∴∠EDC=∠ECD，而∠A+∠ECD=90°，∠EDC+∠ADE=90°，∴∠A=∠ADE.这一问还有别的证法，比上边的复杂，不再陈述，有兴趣的同学自己证一证.

(2)我说过，几何有三宝，勾股、相似和三角，人教版九年级下学期学习，相似与三角函数的知识。我们先用勾股定理算一下，显然得列方程，已知AD=16，DE=10，由(1)知∠A=∠ADE，∴DE=AE，又DE=EC，∴AC=20，在Rt△ADC中，由勾股定理可算出DC=12，设BD=x，在Rt△BDC中，BC²=BD²十DC²，即BC²=x²+12²，在Rt△ABC中，BC²=AB²一AC²，即BC²=(16十x)²一20²，∴x²+12²=(16+x)²一20²，解得x=9，在Rt△BDC中，由勾股定理可算出BC=15.

我们知道，当直角多次出现时，可想到面积，设BC=x，由于S△ABC=AB×DC/2=AC×BC/2，∴AB×12=20x，∴AB=5x/3，∴BD=5x/3一16，在Rt△BDC中，BD²十DC²=BC²，∴(5x/3一16)²+12²=x²，解得x1=x2=15，即BC=15.

下面用三角函数，相似做一下

由分析和∠A=∠BCD，在Rt△ADC中，cosA=AD/AC=4/5，在Rt△BDC中，cos∠BCD=DC/BC=4/5，即12/BC=4/5，∴BC=15.

也可这样，在Rt△ADC中，tanA=DC/AD=12/16=3/4，在Rt△ACB中，tanA=BC/AC=3/4，即BC/20=3/4，∴BC=15.当然也可用正弦函数，余切函数算出来，只不过换一下角度.

用相似做.易知由于∠A=∠BCD，∠BDC=∠ADC，∴△ADC∽△CDB，∴AD/DC=AC/BC，即16/12=20/BC，∴BC=15.(我们看到这与用三角函数做是一致的，这就看你喜欢用哪些知识了)

我们知道通过相似能推出CD²=AD×DB(也称射影定理)，∴DB=12²/16=9，在Rt△BDC中，可算出BC=15.

【总结反思】

本领虽然不难，但可以充分发挥同学们的能力，从不同角度去思考得出同样的结果，我们平时做题时，多加强这方面的练习，以便灵活运用基础知识，熟能生巧，遇到较难的题目也就能各个击破，最终取得可喜的成绩。

感谢大家的关注、转发、点赞、交流！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小故创作整理编辑！