欧拉是怎么发现自然底数e的(欧拉是如何发现欧拉公式的)

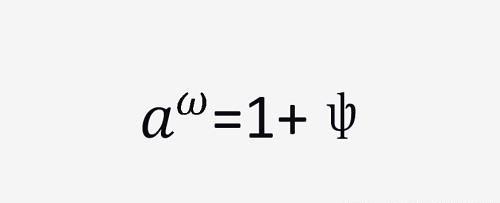
导语：数学新思维：你知道欧拉是如何发现自然常数e的吗？

自然常数的发现是数学上的一个奇迹，它的主要贡献者就是大数学家欧拉，如下是欧拉发现自然常数e的过程，

a大于1时，a的幂随a的增加而增加，且a^0=1,当是无穷小时，即几乎处处等于0时，我们有

ψ是无穷小，当ψ不是无穷小时，就不是无穷小，这说明了和ψ存在一定的关系，我们令ψ=kω，得到

以a为底的对数得到：

我们将上式a^ω=kω+1变形得到:它对任何i都成立

将上式二项式展开得到

如果令i=z/ω，且当ω为无穷小时，i为无穷大时，那么z=iω就是一个有限数，我们将ω用z/i来代替。这时就得到，这里的k如前面所述的，是一个确定的依赖于a的数

当i是无穷大时，即i大于任何给定的数，则我们就得到

我们将上述结论带入a^z的表达式，就得到

这个等式表示了a与k之间的关系，事实上，如果令z=1，我们得到

我们选取a使得k=1，那么就得到我们常用的自然常数e的无穷级数形式

本文内容由快快网络小馨创作整理编辑！