二次函数的值问题有几种类型(含参二次函数的值问题)

导语：二次函数的最值问题

前两篇文章讨论了一元二次方程根的分布问题，而且从初中起我们就开始逐步研究二次函数的性质和图象，今天我们再看一下二次函数另一类我们常碰到的问题-最值问题，有不少最值问题最后都可以化归为二次函数的最值。

二次函数的图象是一条抛物线，解决二次函数的区间最值问题的思路是抓住“两点一轴”，两点即函数的定义区间的两个端点，一轴指的是抛物线的对称轴。结合配方法，根据函数的单调性来求解，经常涉及分类讨论思想。根据二次函数解析式上参数的位置，二次函数的最值问题可以分为以下几类（不含参数变量的类型就不再讨论了）。

1.区间定，轴动-二次函数的定义区间是已知的，但二次函数的对称轴不定（含参）。对此，我们只需按对称轴在区间的左侧、内部、右侧分成三类，结合其图象特征分类求解即可。

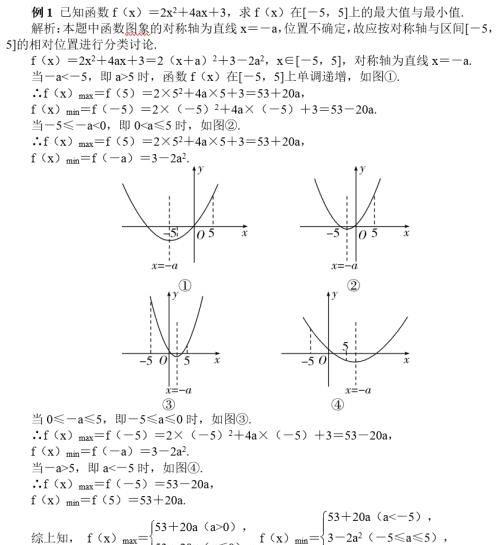
2.轴定，区间动-这种情形与前一种的解法相通，也是按对称轴在区间的左侧、内部、右侧分成三类，结合其图象特征分类求解。

3.区间动，轴动。此时区间和对称轴都不确定，缺少一个参考，因此我们可以先让区间不动，按对称轴在区间左侧、内部、右侧进行讨论，有时在区间内部还可分为两种情况，

一元二次方程根的分布问题（1）

一元二次方程根的分布问题（2)

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小萱创作整理编辑！