圆锥表面取一般位置点的方法(圆锥表面求点的方法)

导语：多种方法速求圆锥尖端到液面高度

题目：有一个下面是圆柱体、上面是圆锥体的容器，圆柱的高是10厘米，圆锥的高是6厘米，容器内水深7厘米，将这个容器倒过来放置时，从圆锥的尖端到液面的高是多少？（如下图）

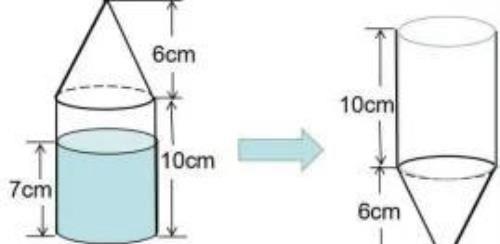
方法一：

解题思路：本题中圆柱、圆锥是等底，不同的是高。所以不必考虑底面积，只要考虑高。圆柱体的高度是10厘米，容器内的水高7厘米。得出：水的体积=圆柱体积的7/10.

等底等高情况下，圆锥体积是圆柱的1/3，而且题中圆锥体的高度是6厘米，圆柱高度是10厘米，得出：圆锥体积=1/3×圆柱体积的6/10=圆柱体积的1/5将这个容器倒过来放，水要先装满下部的圆锥，再淹到圆柱。

水的体积-圆锥体积=圆柱体积的7/10 -圆柱体积的1/5=圆柱的体积5/10说明这时水面已经淹到圆柱的5/10处，圆柱的高是10厘米，水在圆柱的内的水面是5厘米。即：水在圆柱的内的水面高度+圆锥体的高度=从圆锥的顶点到水面的高5+6=11厘米

答：从圆锥的顶点到水面的高为11厘米。

方法二：

解题思路：把圆柱内水的体积分成两部分，根据等底等高的圆柱的体积是圆锥的体积的3倍，所以先把圆柱内6厘米的水的体积的1/3，即高为2厘米的水的体积倒入圆锥中，正好把圆锥部分装满，则剩下的就是圆柱内水的高度，即7-2=5厘米，由圆锥的高度+圆柱内水的高度即可解决问题.

规范解答：6÷3=2（厘米）

7-2=5（厘米）

6+5=11厘米

答：从圆锥的尖到液面的高是11厘米.

方法三：解方程

如下图所示：

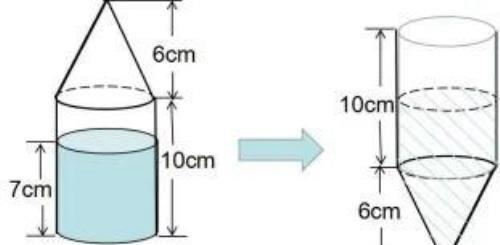
解：设圆柱底面积为S，倒过来放时，圆柱内水的高度为h.

根据液体体积不变列方程如下:

(6S)÷3 + Sh= 7S （等高的圆锥体积是圆柱体积的三分之一)

所以h=5

所以倒过来放时，从圆锥的尖到液面的高是6+5＝11（厘米）。

点评：此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用，这里关键是找出圆柱内高6厘米的水的1/3是指高度为2厘米的水的体积，倒入圆锥容器内正好装满。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小嫣创作整理编辑！