线段和差问题截长补短(线段和差的处理方法)

导语：线段和差如何证，截长补短证相等

下列题目是1993年台湾高中数学竞赛决赛中一道几何证明题：

题：如图1，设M为圆弧AB上的中点，C为弧AMB上异于M的点，且AC＞BC，并设D为自M所作AC的垂线的垂足．

试证：AD＝DC＋BC．

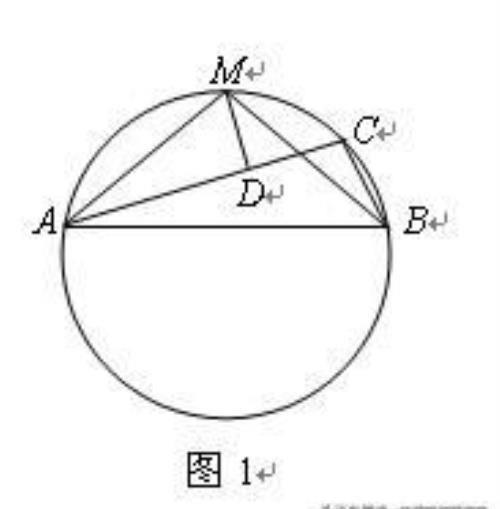
分析：这是线段和差关系的证明题，其证明方法一般有两种——截长法和补短法。

所谓截长法就是在较长的线段上截取一段与较短两条线段中的一条相等，再证剩下的一段与另一条线段相等．

所谓补短法就是把较短两条中的一条延长，把两条较短的线段合并为一条线段，再证合并后的线段等于较长的线段．

这两种证法的总体思路就是“截长”“补短”证相等。

下面分别用这两种方法对该题进行证明。

方法一：截长法

由于AD较长，故在AD上截取一段与DC（或BC）相等的一段，然后再证明AD上剩下的一段等于另一条线段BC（或DC）即可．此时有如下两种证法：

证1（在AD上截取与DC相等的一段）。由于MD⊥AC于D，故在AD上截取DE＝DC，可得MD是CE的垂直平分线（注意不要截取AE=DC，否则缺乏特殊性），连结MC、ME（如图2）.

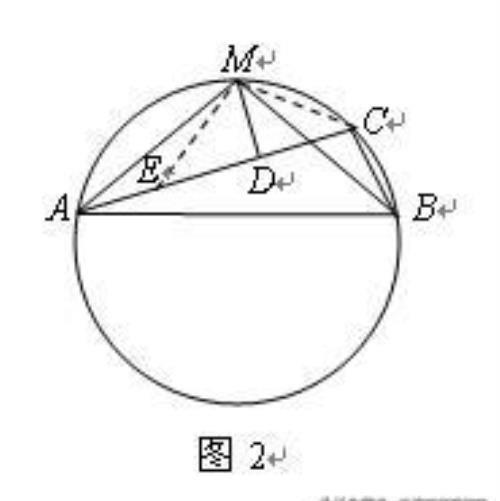
则由已知，得MD垂直平分CE，

所以ME＝MC，

所以∠MEC=∠MCA，

因为M是弧AB的中点，

所以MA＝MB；

设弧AM的度数为2m，弧BC的度数为2n，

则弧CM的度数为2(m－n)，

所以∠AME＝∠MEC－∠MAC＝∠MCA－∠MAC

＝m－(m－n)＝n＝∠BMC．

即∠AME=∠BMC，

所以ΔAME≌ΔBMC，

所以AE＝BC，

所以AD＝AE＋DE＝BC＋DC．

证2（在AD上截取与BC相等的一段）

如图2，在AD上截取AE＝BC（之所以不截取DE=BC是因为考虑到MD垂直AD），连结MC，ME．

在ΔMAE与ΔMBC中，

MA＝MB，AE＝BC，∠MAE＝∠MBC，

∴ΔMAE≌ΔMBC，

∴ME＝MC，

∴ΔMEC是等腰三角形，

又MD是底边上的高，

所以DE＝DC，

所以AD＝DC＋BC．

方法2：补短法：

由于DC、BC较短，把它们并为一条，再证合并后的线段等于AD即可．此时有如下两种证法：

证3（在DC上补BC）

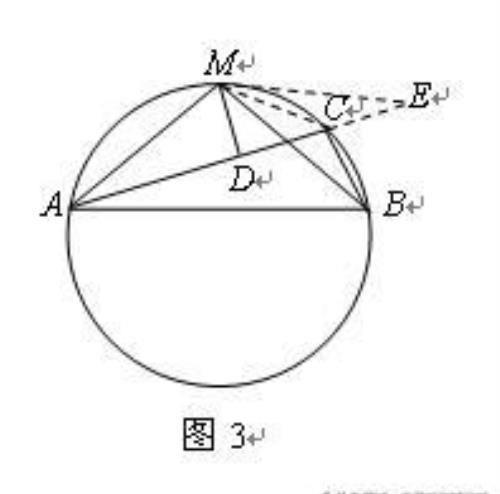
如图3，延长DC到E，使CE＝BC（下面只须证明DE＝AD即可）．

连结ME，MC，在ΔMBC与ΔMEC中，

因为∠MCE与∠MCA互补，

∠MCB与∠MAB互补，

又∠MCA＝∠MBA＝∠MAB，

所以∠MCE＝∠MCB，

又MC＝MC，BC＝EC，

∴ΔMCE≌ΔMCB，

∴ME＝MB＝MA，

又MD＝MD，

故RtΔMDE≌RtΔMDA，

所以DE＝AD，

所以AD＝DC＋BC．

证4　如图4，延长BC到E，使CE＝CD，连结ME，MC．

在ΔMCE与ΔMCD中，

∠MCE＝∠MAB＝∠MBA＝∠MCD，

又CE＝CD，MC＝MC，

∴ΔMCE≌ΔMCD，

∴ME＝MD，∠E＝∠MDC＝Rt∠，

∴RtΔMAD≌RtΔMBE，

∴AD＝BE＝DC＋BC．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小樊创作整理编辑！