导语：判断推理难点突破系列——推出式的证明

上一期张老师给大家介绍了判断推理里的集合推理是什么、集合推理题目的判定方法以及最后让大家熟记的6条推出式，那本期张老师就给大家解释一下这六个推出式。

集合推理

（1）所有S是P→某个S是P→有的S是P

这个推出式子其实很好理解，举个例子，现在有一个命题：“我们班所有同学都吃了早饭”为真，一定能推出“某个（小明）吃了早饭”这个命题为真，当然也能推出“有的同学吃了早饭。”

（2）所有S是P→有的P是S

对于这条推出式，我们借用下欧拉图来理解。首先画出“所有S是P”的欧拉图，如下：

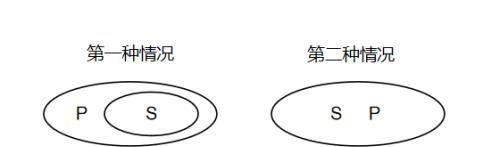
所有S是P→有的P是S

观察也不难发现，这两个欧拉图也可以表示“有的P是S”，这也就是“所有S是P→有的P是S

”的由来。

（3）所有S是P→所有不是P的不是S

我们继续借用上面的“所有S是P”的欧拉图来理解，如下：

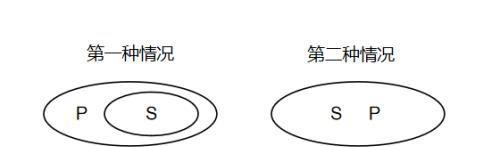
所有S是P→所有不是P的不是S

观察同样可以发现，这两个欧拉图也可以表示“所有不是P的不是S”

（4）所有S不是P→某个S不是P→有的S不是P

这个推出式和（1）式相对，那我们就借用（1）式的例子来理解，“我们班所有同学都没吃早饭”为真，一定能推出“某个（小明）没吃早饭”这个命题为真，当然也能推出“有的同学没吃早饭。”

（5）所有S不是P→所有P不是S

首先画出“所有S不是P”的欧拉图，如下：

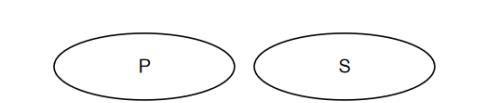
所有S不是P→所有P不是S

我们也能观察出来，既然所有S不是P，那么所有P当然也不是S。

（6）有的S是P→有的P是S

对于这个最后的也是最难的推出式，我们同样通过画欧拉图的方法来理解。“有的S是P”欧拉图如下：

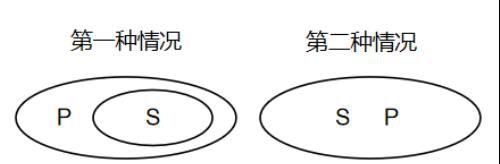
有的S是P→有的P是S

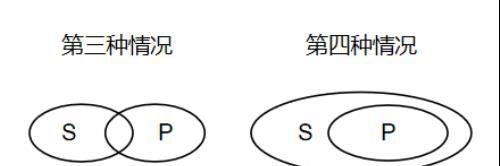
有的S是P→有的P是S

这四种情况都可以表示“有的S是P”，当我们将图中S和P的位置进行调换发现，刚好又符合了“有的P是S”，所以可以证明“有的S是P→有的P是S”是正确的。

最后这个最难理解，很多同学会记成“有的S是P→有的S不是P”，这个是错误的、是推不出的。请考生一定要记清楚。

通过对这六条推出式的证明，大家能深度理解了这六条推出式，一定要牢记~

判断推理难点突破系列——消连关系讲解

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！