值问题例题(值问题讲解)
导语:「最值问题」最值问题探究
从各区的模考卷来看,最值问题仍是中考热门,本文以各区一、二模卷中最值问题为例,对最值问进行简要分类和例析。
一、最值类型
1、将军饮马型:通常为两条线段之和的最值问题,利用对称性质将其中
一条线段进行转换,再利用两点之间线段最短(或三角形三边关系)得到结果。
2、小垂回家型:通常为一条线段的最值问题,即动点的轨迹为直线,利用垂线段最短的性质得到结果。
3、一箭穿心型:通常为一条线段的最值问题,即动点的轨迹为圆或弧,利用点与圆的位置关系得到结果。
4、一加半型:通常为一条线段与另一条线段一半的和的最值问题,即将那半条线段利用三角形中位线或30°的对边等知识进行转换,再利用饮马或小垂或穿心。
5、三边关系型:通常利用两边之和大于第三边、两边之差小于第三边,求其最大(小)值。
6、综合型:大多为饮马+小垂、小垂+穿心、饮马+穿心、饮马+转换等。
二、分类例析
1、饮马型
例1:如图,在正方形ABCD中,点E在CD上,CE=3, DE=1, 点P在AC上,则PE+PD的最小值是_____
解析:如图
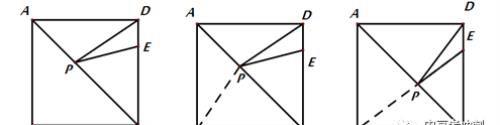
例2:如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为____.
解析:如下图
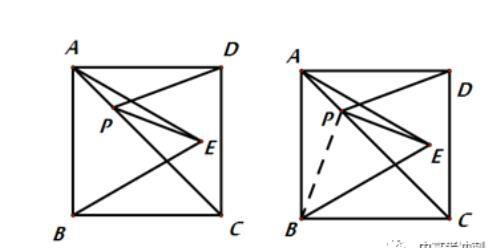
2、小垂型
例3:如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为_________.
解析:如下图
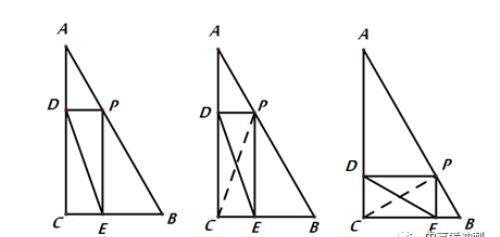
3、穿心型
例4:如图,在边长为4的菱形ABCD中,∠ABC=120°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN翻折得到△A’MN,连接A’C,则A’C长度的最小值是____.
解析:如下图
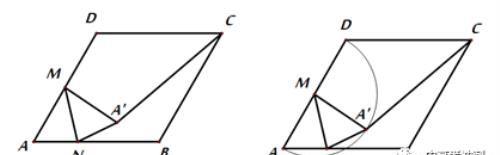
4、转换型
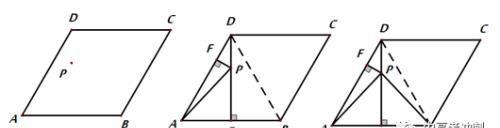
例5: 如图,P为菱形ABCD内一点,且P到A、B两点的距离相等,若∠C=60°,CD=4,则的最小值为____________
解析:因为P到A、B两点的距离相等,所以P 在AB的垂直平分线上,又因菱形ABCD中∠C为60°,所以△ABD为等边三角形,AB的垂直平分线经过点D,如下图
由∠ADP=30度,可将PD的一半进行转换,即过点P作AD的垂线。如图,
即B、P、F三点共线,且BF⊥AD时最短
5、三边型
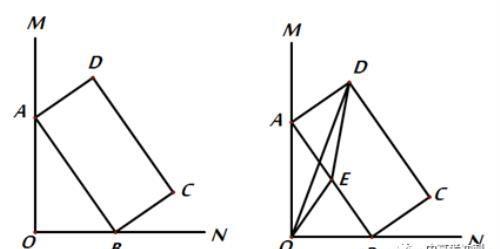
例6:如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为________
解析:如下图因为AB为定长,所以取其中点E,则OE为定值,在△ODE中,DE为定值,OE为定值,根据三角形三边关系即可得到OD的最大值。
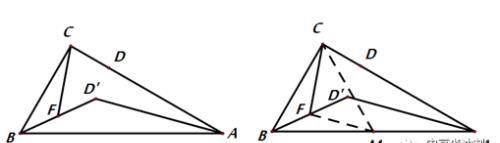
例7:如图,已知△ABC中,∠ACB=90°,BC=4,AC=8,点D在AC上,且AD=6,将线段AD绕点A旋转至AD’,F为BD’的中点,连结CF,则线段CF的取值范围.
解法一:瓜豆原理,点F的轨迹为圆,一箭穿心便可以求出其取值范围。
解法二:如下图,取AB的中点M,连接FM,CM,由斜边上的中线等于斜边的一半得CM为定值,由三角形中位线得FM为定值,所以在△CFM中,三边关系可得到CF的取值范围.
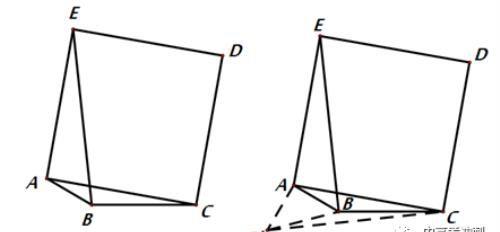
例8:如图,BA=1,BC=2,以AC为一边做正方形AEDC,使E,B两点落在直线AC的两侧,当∠ABC变化时,求BE的最大值.
解析:将△AEB以点A中心顺时针旋转90°,得到△ACB’,如下图所示,连接BB’,所以B’C=BE,在△BB’C中,BB’为定值,BC为定值,三角形三边关系即可得到B’C的最大值,即BE的值.
6、结合型
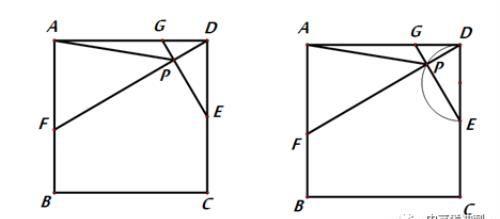
例9:如图,正方形ABCD中,AB=4, E为CD边的中点,F、G为AB、AD边上的点,且AF=2GD, 连接E、DF相交于点P,当AP为最小值时,DG=________
解析:由AF=2GD,AD=2DE,得△AFD∽△DGE.如下图
∴GE⊥DF, 那么线段AP中,A点为定点,P为动点,由∠DPE为直角,所以P的轨迹为一以DE中点为圆心的一段弧。如下图
由一箭穿心可得到AP的最小值为A,P,M三点共线,而此时,由△DMP∽△FAP可得到AP=AF即可得到结果.
三、模考分析
如图,在平面直角坐标系中,A(6,0),B(0,8),点C在y轴正半轴上,点D在x的正半轴上,且CD=6,以CD为直径在第一象限作半圆,交线段AB于点E、F,则线段EF的最大值为______如图,在平面直角坐标系中,A(6,0),B(0,8),点C在y轴正半轴上,点D在x的正半轴上,且CD=6,以CD为直径在第一象限作半圆,交线段AB于点E、F,则线段EF的最大值为______
解析:线段EF由于半圆的变化而变化,所以应将其作为弦的变化来看,而弦长又与弦心距存在变量之间的关系,所以首先作出弦心距.如下动图,所以当PQ最小时,EF最大。
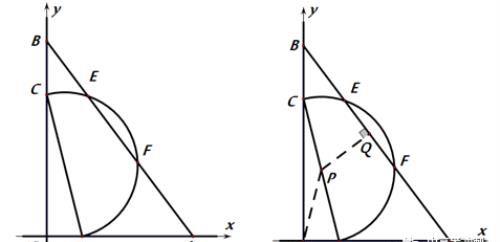
方法一:穿心+小垂(P点为以O点圆心,OP为半径的弧上)求出OQ的最值,即PQ的最小值,再由勾股定理和垂径定理可求得EF.
方法二:三边+小垂(三角形OPQ)求出OQ的最值……
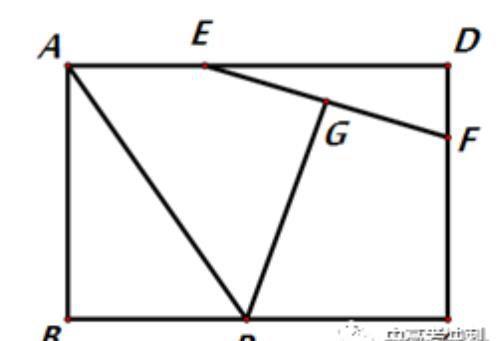
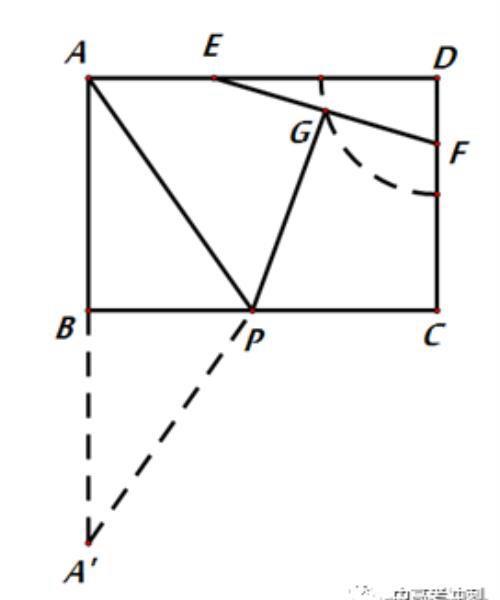
如图,矩形ABCD中,AB=2,AD=3,点E,F分别为AD,DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点.则PA+PG的最小值为( )
A.3 B.4 C.2√5 D.5
解析:因为G为EF的中点,EF=2,所以点G的轨迹为以D为圆心DG为半径的弧, 【饮马+穿心】即A’,P,G,D四点共线时,PA+PG最小(PA+PG=PA’+PG+DG)
四、趁热打铁
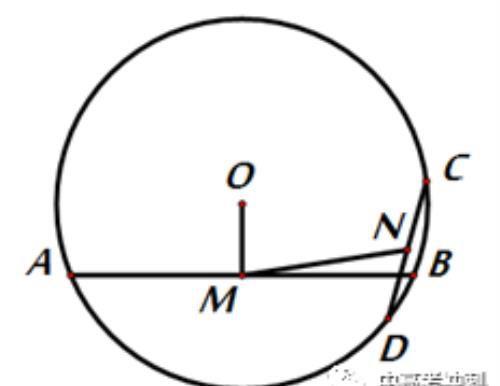
【练习1】如图,已知圆O的半径为13,弦AB长为24,弦CD长为10,点N为CD的中点,O到弦AB的距离为OM,则MN的最小值是________
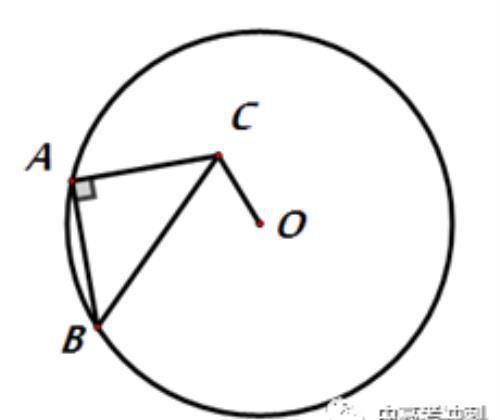
【练习2】如图,A,B为圆O上两点,以AB边直角边作等腰直角三角形ABC,若圆O的半径为5,则OC的最小值为
历史回顾
【方法探究】共圆模型
【方法探究】定角夹定高(探照灯模型)
【方法探究】二次函数与相似三角形存在性的问题
【解题方法】一道二次函数的动点问题探究
【期中备考】动点问题-平行线的性质与判定的综合
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小琪创作整理编辑!