正三角形在正方形中(求正方形中三角形的面积)

导语：正方形中的正三角形，不满足于一种方法利于扩展思路

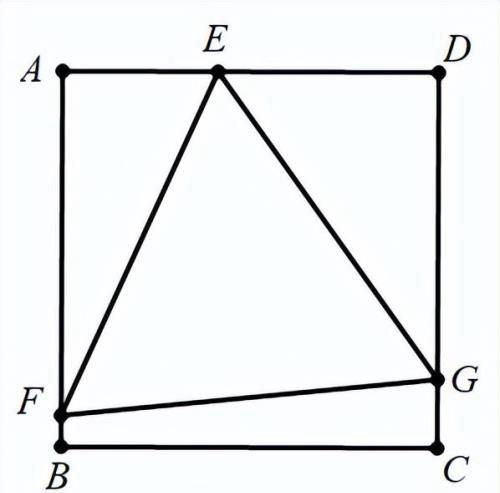
如图，正方形ABCD中，E、F、G三点分别在边AD、AB、CD上，且△EFG为等边三角形，

若AF=5，DG=6，则正方形的边长为___________

方法一：一线三角，全等

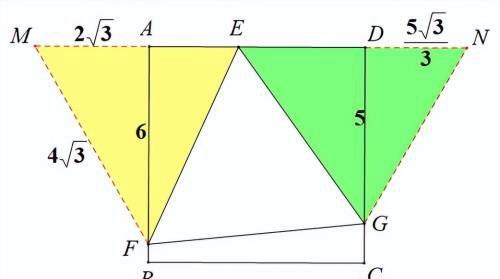
在直线AD延长线上分别取点M、N，使∠AMF=∠DNG=60°

易知∠MEF+∠NEG=120°，∠MEF+∠MFE=120°得∠NEG=∠MFE

EF=EC，故△EFM≅△GEN

而EN=MF=4√(3)，故DE=(7√(3)/3)

ME=GN=(10√(3)/3)，故AE=(4√(3)/3)

故AD=(11√(3)/3)

点评：此法是主流方法，对学生而言通俗易懂且方法比较巧妙，成为很多命题灵感的源.

方法二：一线三角，相似

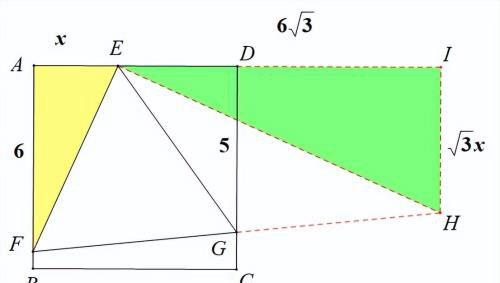
过点E作EH⊥EF交FG的延长线于点H，

作HI⊥AD，易知△AEF~△IHE且相似比为1：√(3)

设AE=x，则HI=√(3)x，易知G为FH的中点，

AF||DG||HI，故DG为梯形AFHI的中位线，

得x=(4√(3)/3),故AD=(11√(3)/3)

点评：正三角形，除去本身的特殊性质，常常要考虑构造成特殊的直角三角形来解决问题；例如放在坐标系的正三角形，反比例函数中的正三角形，皆可利用此法；

方法三：与方法二一样，同学们可自行推导计算；

方法四：共圆

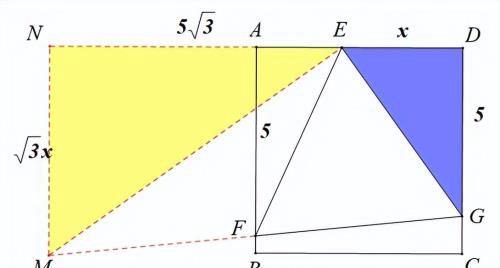
作EH⊥FG于点H，连接AH、DH，

∠FAE=∠EHF=90°，故A、F、H、E四点共圆，

故∠HAQ=60°，同理可得∠HDA=60°

故△AHD为等边三角形，作HQAD于点Q，

H为FG的中点，HQ||AD||DG，故HQ=(11/2)

故AD=(11√(3)/3)

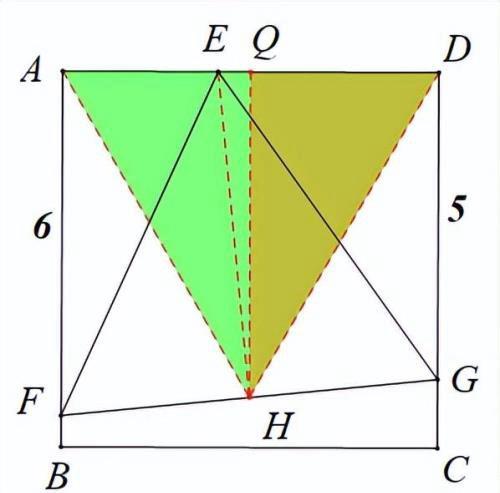
点评：此法利用共圆亦也快速解决边长问题，共圆的条件是利用此法的关键，对于学霸，这些方法应该纳入方法库中.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小心创作整理编辑！