勾股定理之折叠问题知识点(勾股定理中的折叠问题易错点是什么)
导语:勾股定理及其逆定理(四)——折叠问题与等面积法

【思路点拨】
1 请填写“勾股定理”或“勾股定理逆定理”:
条件是直角三角形时,考虑______________________;
要证明三角形是直角三角形,考虑______________________.
2折叠的性质:
① 叠是全等变换,折叠前后对应角______,对应边_____;
②折叠前后对应点所连的线段被对称轴____________.
3 等面积法
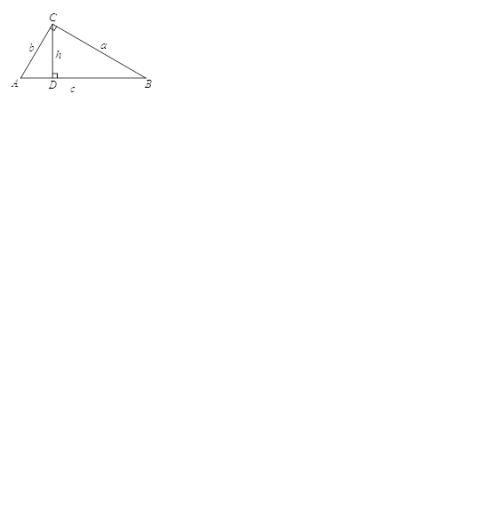
如图,Rt△ABC的面积可以表示为_____________,还可以表示为_______________,根据面积的不同表达形式,可以得到a,b,c,h之间的数量关系为___________________________.
4 折叠问题处理思路
(1)找__________________;
(2)____________________;
(3)利用_______________列方程.
5 等面积法
当几何图形中出现多个高(垂直、距离)的时候,可以考虑______________解决问题,即利用图形面积的不同表达方式列方程.
6做一做:
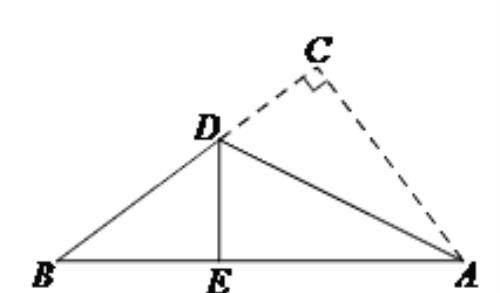
如图,有一张直角三角形纸片,两直角边AC=6,BC=8,点D在BC边上,将直角边AC沿直线AD折叠,点C恰好落在斜边AB上的点E处.设DE的长为x,则CD=__________,BD=_________.(用含x的代数式表示)
【例题示范】
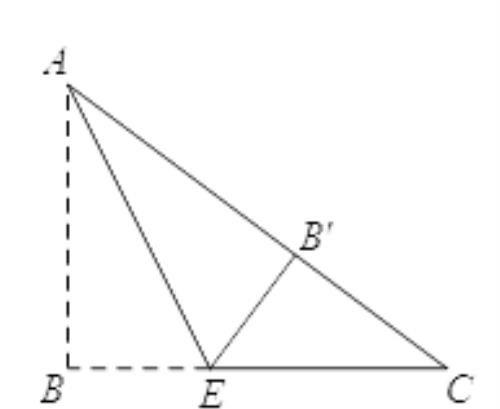
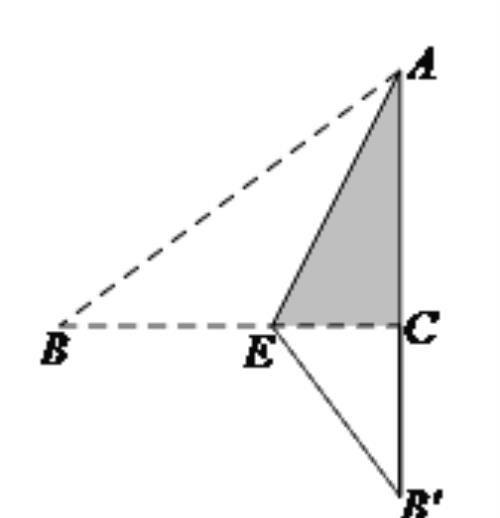
如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC沿过点A的直线折叠,使点B恰好落在AC边上的点B′处,若折痕交BC于点E,则B′E的长为_________.
思路分析:
1找折痕:直线AE即为折痕
2转移,表达设B′E=x,则CE=4-x,由折叠,得BE=B′E=x,AB′=AB=3
在Rt△ABC中,∠B=90°,AB=3,BC=4, 由勾股定理,得AC=5 ∴B′C=2
3利用勾股定理列方程在Rt△EB′C中,由勾股定理,得
x2+22=(4-x)2 解得x=1.5
【巩固提高】
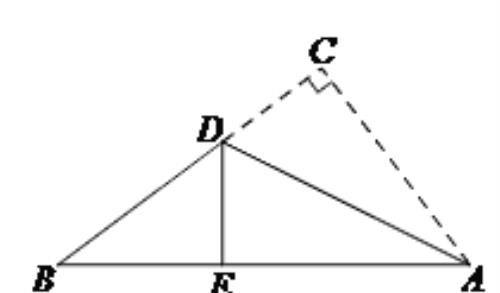
1 如下图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,将直角边AC沿直线AD折叠,点C恰好落在斜边AB上的点E处,则线段CD的长为__________.
2 如下图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长为__________.
3 如下图,在长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为_________.
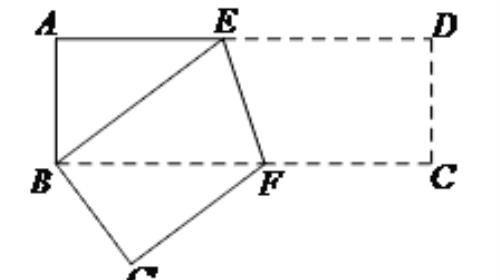
4. 如下图,折叠长方形的一边AD,使点D落在BC边上的点F处,若AB=4cm,BC=5cm,则EF的长为________.
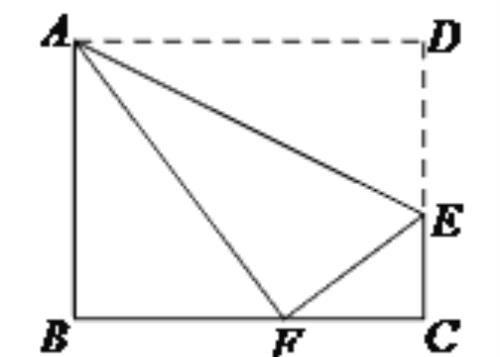
5 如下图,在△ABC中,AB=20,AC=12,BC=16,E为BC边上一点,把△ABC沿AE折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.
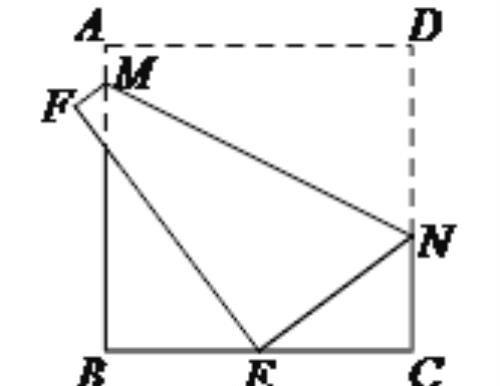
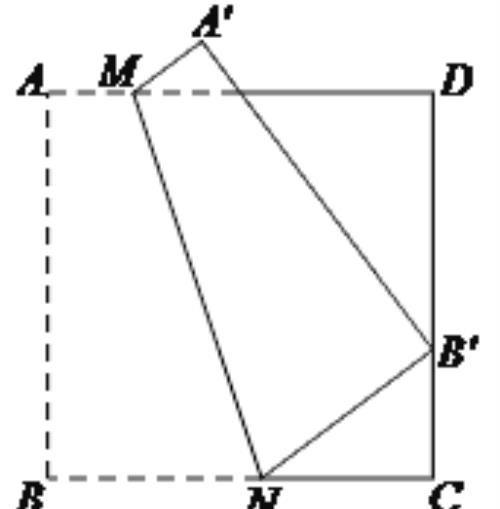
6如下图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B'处,点A的对应点为A'.若B'C=3,则CN=______,AM=_______.
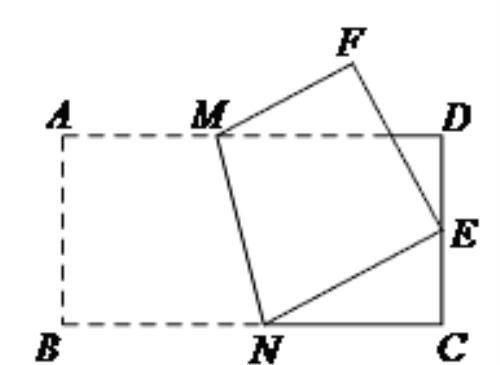
7如图,将长为4cm,宽为2cm的矩形纸片ABCD折叠,使点B落在CD边的中点E处,压平后得到折痕MN,则线段AM的长为__________.
8、若直角三角形两直角边的比为5:12,则斜边上的高与斜边的比为( )
A.60:13 B.5:12 C.12:13 D.60:169
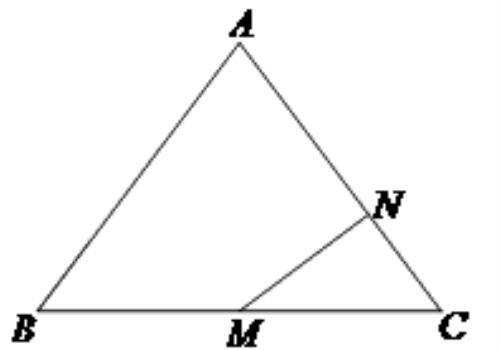
9如下图,在△ABC中,AB=AC=5,BC=6,M为BC边的中点,若MN⊥AC于点N,则MN=__________.
10、若直角三角形两条直角边的长分别为7和24,在这个三角形内有一点P到各边的距离都相等,则这个距离是__________.
11已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC+BC=14cm,AB=10cm,则CD=__________.
12若等腰三角形底边上的高为8,周长为32,则该等腰三角形的面积为__________.
【拓展训练】
1 观察图中的3个图案,设△ABC的三边长分别为a,b,c,请根据三角形的形状,猜测a2,b2,c2满足的条件.
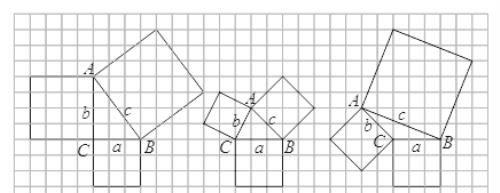
(1)如果△ABC是直角三角形,则a2+b2______c2;
(2)如果△ABC是锐角三角形,则a2+b2______c2;
(3)如果△ABC是钝角三角形,则a2+b2______c2.
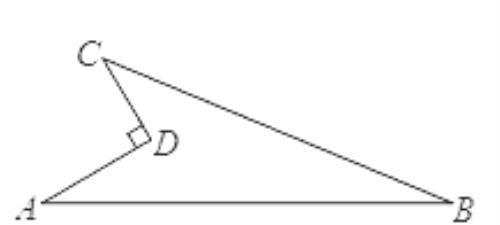
2如下图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.
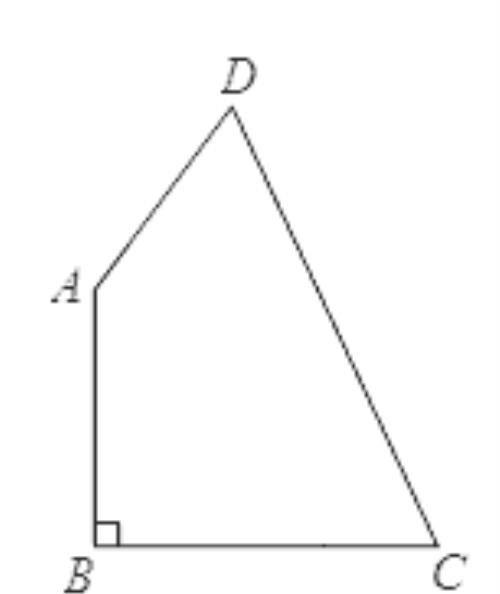
3如下图,一块四边形菜地ABCD,已知∠B=90°,AB=9m,BC=12m,AD=8m,CD=17m.求这块菜地的面积.
【参考答案】
【思路点拨】
1 勾股定理,勾股定理逆定理
2 ①对应边相等,对应角相等
②垂直平分
3 ½ab ,½ch,ab=ch
4 (1)折痕
(2)表达、转移
(3)勾股定理
5 利用面积相等
6 x,8-x
【巩固提高】
1 3 cm
2 3 cm
3 6
4 5/2cm
5 36
6 4,2
7 13/8cm
8 D
9 12/5
10 3
11 4.8 cm
12 48
【拓展训练】
1 (1)= (2)> (3)<
2 216 m2
3 这块菜地的面积为114 m2
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小碧创作整理编辑!