立体几何轨迹和值问题(轨迹思想解几何值)

导语：颇有个性的几何轨迹与最值问题“三例说”

在平面几何有关最值问题中，一般情况下：首先，确定动点的轨迹；然后，再求相应的最值。而动点的轨迹，千变万化，难易悬殊，有的规律显见，有的隐蔽难寻，更有颠覆认知，极具个性。现选编三例说说其的特性，供参考。

【例一】（如图）在平面直角坐标系中，点B是x轴上一动点，C（0，2√3），∠ACB=60º，S△ABC=3√3，求：线段OA的最小值。

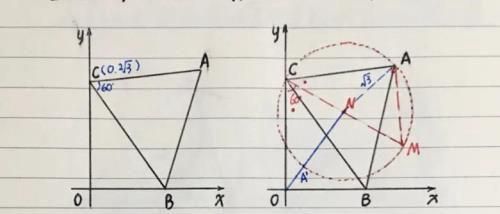
【分析】首先，主动点B，轨迹为直线，所在△OCB，从动点A，所在△CBA，形状为∠BCA=60º，面积3√3；然后，应用“瓜豆”思维逻辑，作辅助线段CM；最后，得到点A的轨迹，并非直线而是圆弧（非“瓜豆”，有个性）…（过程见下）

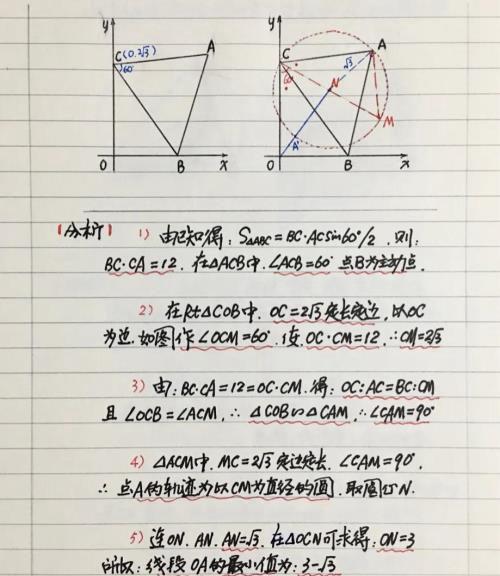
【例二】（如图）△ABC中，∠ACB=60º，AB=3√3，△ABC所在外接圆⊙O，若将AC边所对弧沿弦AC折叠，与边AB交于点D，则取弧AD的中点M，连接OM，求：OM的最小值。

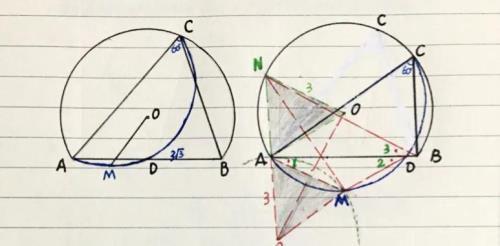
【分析】首先，点C轨迹（定角对定弦）为△ABC外接圆，此题极有个性，主动点须重新寻找；然后，取点N为主动点，所在△OAN，从动点M，所在△ANM，形状确定；最后，运用“瓜豆原理”确定点M的轨迹…（过程见下）

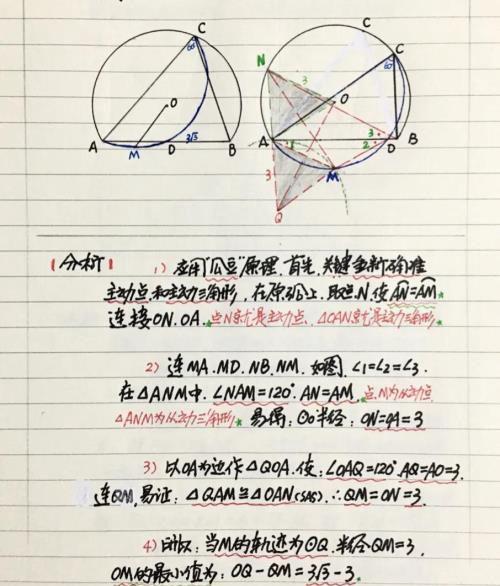
【例三】（如图）△ABC中，BC=2，D是AC上的一点，且有∠ABD=∠ACB，点E与点D关于AB为对称轴对称，连接CE，若△ABC的面积为1，则CE的最小值为多少？

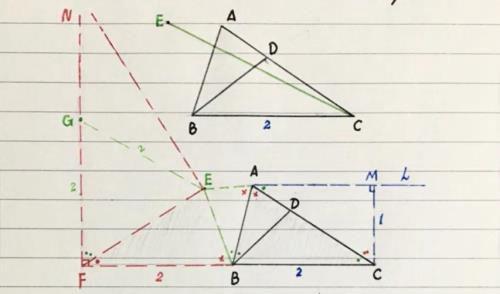
【分析】首先，主动点A，轨迹为直线L，L∥BC，从动点E，由题意找出相似三角形；然后，构造△BFE∽△ACB，FE×CA=4（此题轨迹非一般认知）；最后，利用线段长度再造△FNE∽△CAM…（过程见下）

以上分析“三例说”，“道听度说”供参考。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！