导语：小升初数学︳分清题型理清细节掌握解题思路解决植树问题不出错

 一、基本知识点

1、含义

按相等的距离植树，在全长、棵距、棵数这三个数量中，已知其中的两个量，

求第三个量的应用题，叫作植树问题。

2、特点（空，即间隔）

两端植树：树多空少，少一个；

两端不植树：树少空多，多一个；

一端植树：树、空一样多；

封闭图形植树：树、空一样多。

3、题型

（1）线上植树，线上植树又可分为非封闭线路上的植树和封闭线路上的植

树两种情况。

（2）平面植树。

（3）特殊的植树问题：例如：敲时钟、锯木头、爬楼梯、列队等与间隔有

关的问题。

4、数量关系

（1）线上植树

○1 在非封闭线路上的植树问题：

A、两端都植树，则植树的棵数比间隔数多1，其基本关系式为：

棵数=间隔数+1=全长÷棵距+1

全长=棵距×（棵数-1）

棵距=全长÷（棵数-1）

B、一端植树、另一端不植树，则植树的棵数与间隔数相等，其基本关系式

为：

棵数=间隔数=全长÷棵距

全长=棵距×棵数

棵距=全长÷棵数

C、两端都不植树，则植树的棵数比间隔数少 1，其基本关系式为：

棵数=间隔数-1=全长÷棵距-1

全长=棵距×（棵数+1）

棵距=全长÷（棵数+1）

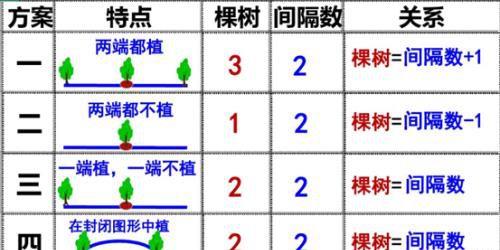
○2 在封闭线路上的植树问题。

A、环形线路：它没有端点的问题，所以棵数与间隔数相等，其基本关系式

为：

棵数=间隔数=全长÷棵距

全长=棵距×棵数

棵距=全长÷棵数

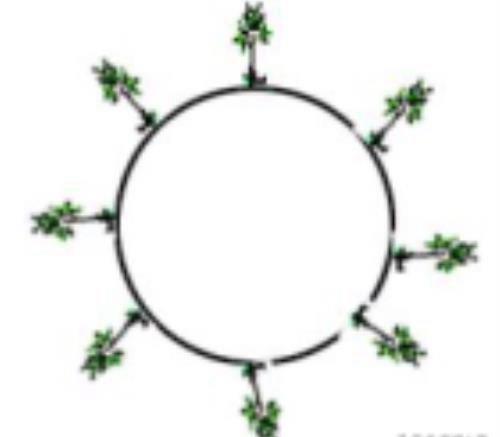
B、方形线路：4个角上都要植树，那么 4个角上的算了 2遍，其基本关系

式为：

棵数＝全长÷棵距-4

棵数=（每边的棵数－1）×边数

棵树= 每边的棵数×边数－顶点数

C、等边三角形

棵数＝全长÷棵距-3

（2）平面植树

棵数=占地总面积÷每棵树占地面积=占地总面积÷（棵距×行距）

5、解题思路

先弄清楚植树问题的类型，然后可以利用公式。

6、解题关键

（1）分清种类（线形、环形）；

（2）理清细节（一旁、两旁）；

（3）先求间隔数（锯木头先求次数）。

7、解题方法、步骤

要理解，学画图，看手指：手指为树，指缝为空（间隔）。

（1）已知棵数与棵距， 求植树的总长度。

第一步：求空的个数（即间隔数）

看清题意，分析是怎样植树；

若两端植树，就用棵数减 1；

若两端不植树，就用棵数加 1；

若是封闭图形，棵数即是空数（间隔数）。

第二步：求植树的总长度

棵距×空数（间隔数）＝总长度

（2）已知植树总长度与棵距，求棵数。

第一步：求空的个数（间隔数）

总长度÷棵距＝空数（间隔数）

第二步：求棵数

看清题意，分析是怎样植树；

若两端植树，就用空数加 1；

若两端不植树，就用空数减 1；

若是封闭图形，空数即是棵数。

（3）已知植树总长度与棵数，求棵距。

第一步：求空数（间隔数）

与第一种类型相同，

看清怎样植树，

确定是用棵数加1或减1，或不加不减，求出空数。

第二步：求棵距

总长度÷空数（间隔数）＝棵距

 二、一张思维导图归纳总结

 三、经典应用

例1、一条公路的一旁连两端在内共有树91棵，每两棵中的距离是5米，这条公路有多长?

【分析】这是非封闭线路上两端植树问题，已知植树的棵数与棵距，求这段路的总长。

由于两端都植树，所以棵数=间隔数+1。根据公式全长=棵距×（棵数-1）可求这条公路的长度。

【解答】5×（91-1）=450（米）

答：这条公路长 450 米。

例 2、在相距 100 米的两楼之间栽树，每隔 10 米栽 1棵，共栽了几棵？

【分析】因为在两楼之间栽树，紧靠两楼，也就是两端不应栽树、所以栽树

的棵数比可分间隔数少 1。根据公式棵数=间隔数-1=全长÷棵距-1 可求出共栽了

几棵树。

【解答】100÷10-1=9（棵）

答：共栽了 9棵。

例 3、马拉松比赛全程约 42km。平均每 3km 设置一处饮水服务点（起点不设，

终点设），全程一共有多少处这样的服务点？

【分析】这是非封闭线路上一端植树问题。根据公式棵数=间隔数=全长÷棵

距可以求出全程一共有多少处服务点。

【解答】42÷3=14（处）

答：全程一共有 14 处这样的服务点。

例 4、一个湖泊周围长 800 米，沿湖泊周围每隔 3米栽 1棵柳树，每两棵柳

树中间栽 1棵桃树，湖泊周围栽柳树和桃树名多少棵？

【分析】已知条件告诉我们，每隔 3米栽 1棵柳树，每两棵柳树之间栽 1

棵桃树，说明每两棵桃树之间的间隔与每两棵柳树之间的距高是相等的，都是 3

米，植两种树的总长是相等的，都是湖泊周围的长 1800 米。此题属于在封闭线

路上的植树问题，根据公式棵数=全长÷棵距求出湖泊周围栽多少棵柳树和桃树。

【解答】1800÷3=600（棵）

答：湖泊周围栽柳树和桃树各 600 棵。

例 5、正方形操场四周栽了一圈树，四个角上都栽了树，每两棵树相隔 5米。

甲、乙从一个角上同时出发，围绕操场向不同的方向走去，甲的速度是乙的 2

倍，乙在拐了一个弯之后的第 5棵树与甲相遇（把角上的树看作第一棵树），操

场四周栽了多少棵树？

【分析】因为甲的速度是乙的 2倍，乙走了操场的一条边，甲就走了两条边，

乙拐了一个弯之后走到第5棵树，实际走了4个间隔，那么甲应该走了8个间隔，

相的树就是甲第 2次拐弯以后走到的第 9棵树，所以一边有 5+9-1=13 棵树。根

据正方形线路上 4个角植树，棵数=（每边的棵数－1）×边数，可以求出操场四周

栽了多少棵树。

【解答】每边棵树：5+（5-1）×2=13（棵）

共栽树：（13-1）×4=48（棵）

答：操场四周栽了 48 棵树。

例 6、某城有一条电车路线长 8000 米，从起点到终点共设 17 个电车站，平

均每两个车站间的距离是多少米？

【分析】这是在一条路线上设置车站的问题。这种问题也可以用植树问题的

数量关系来解答。此题属于不封闭线路两端植树问题。要想求每两个车站间的距

离，必须知道总长和可分间隔数。

【解答】8000÷（17-1）=500 米）

答：平均每两个车站间的距离是 500 米。

例 7、某校参加运动会的学生有 1000 人，排成 10 路纵队、前后每两人间隔

1米，这个队伍长多少米？

【分析】把 1000 人排成 10 路纵队，每路有 1000÷10=100 人，100 人之间

有多少个间隔呢？这道题虽然是排队的问题，但是思路和植树问题是相同的。100

个人前后有 100-1=99 个间隔，题目中告诉了每两人的间隔是 1米，这个队伍的

长度就可求了。

【解答】每路纵队人数：1000÷10=100（人）

每路纵队间隔：100-1=99（个）

队伍长度：1×99=99（米）

答：这个队伍长 99 米。

例 8、有一路电车的起点站和终点站分别是甲站和乙站，每隔 5分钟有一辆

电车从甲站出发开往乙站，全程要 15 分钟。有一个人从乙站出发沿电车路线骑

车前往甲站，他出发的时候，恰好有一辆电车到达乙站，在路上，他又遇到了

10 辆迎面开来的电车才到达甲站，这时候，恰好又有一辆车从甲站开出，问：

他从乙站到甲站用了多少分钟？

【分析】这个人前后一共看见了 10+1+1=12 辆电车，每两辆车的间隔是 5

分钟，开出 12 辆电车共有 12-1=11 个间隔，这样可以计算出从第 1辆电车开出

到第 12 辆电车开出的所用的时间，共有 5×11=55 分钟。由于他出发的时候，第

1辆电车已到达乙站，所以这个人从乙站到甲站用了 55-15=40 分钟

【解答】12 辆电车间隔：12-1=11（个）

所有电车开出所用时间：5×11=55（分钟）

此人所用时间：55-15=40（分钟）

答：他从乙站到甲站用了 40 分钟。

这道题除了这种解法，还可以通过画网格图解决。

由图可知，这个人从乙站到甲站用了 55-15=40（分钟）。

例 9、一列火车长 450 米，铁路沿线的绿化带两棵树之间相隔 3米，这列火

车从车头到达第 1棵树到车尾离开第 101 棵树用了 0.5 分钟。这列火车每分钟行

多少米？

【分析】第 1棵树到第 101 棵树之间共有 100 个间隔，所以第 1棵树与第

101 棵树相距 3×100=30 米，火车经过的总路程为 450+300=750 米。已知路程和

时间，根据公式速度=路程÷时间，可以求出这列火车每分钟行多少米。

【解答】路程：（101-1）×3+450=750（米）

速度：750÷0.5=1500（米）

答：这列火车每分钟行 1500 米。

例 10、科学家进行一项试验，每隔 5 小时做 1 次记录，做第 12 次记录时，

挂钟时针指向 9。问做第一次记录时时针指向几？

【分析】第 1次记录到第 12 次记录，中间有 12-1=11 个间隔，每次间隔是

5小时，共用时间为 5×（12-1）=55 小时。由于时针每 12 小时转一周，所以在

48 小时前也是指向 9时，第 12 次记录时是 9点，倒推 55 小时应为 55-48=7 小

时，因此时针指向 9-7=2。

【解答】所用时间：5×（12-1）=55（小时）

转 4 圈后剩：55-4×12=7（小时）

时针指向：9-7=2（时）

答：第一次记录时时针指向 2。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小思创作整理编辑！