费马点的问题(费马问题和费马点问题有什么区别)

导语：再探费马点问题

上次介绍了费马点的问题，很多人在后台留言，希望能够知道怎么找费马点，还有就是多提供几道例题，下面给出找费马点的一种方法（方法很多）和有关费马点的两道例题。

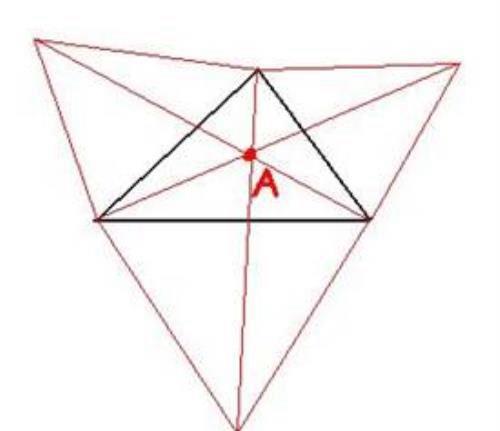
费马点的找法：以三角形的三边向外分别作等边三角形，然后把外面的三个顶点与原三角形的相对顶点相连，交于点A，点A就是原三角形的费马点；

若三角形有一内角大于或等于120度,则此钝角的顶点就是所求的费马点；当△ABC为等边三角形时,此时内心与费马点重合 。

例1：如图，在△ABC中，∠ACB=90°，点P为△ABC内一点.以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，连接PA、PB、PC，当AC=3，AB=6时，根据此图求PA+PB+PC的最小值.

证明：如图，当C、P、M、N四点共线时，PA+PB+PC最小，由旋转可得，△AMN≌△APB，

∴PB=MN

易得△APM、△ABN都是等边三角形，

∴PA=PM

∴PA+PB+PC=PM+MN+PC=CN，

∴BN=AB=6，∠BNA=60°，∠PAM=60°

∴∠CAN=∠CAB+∠BAN=60°+60°=120°，

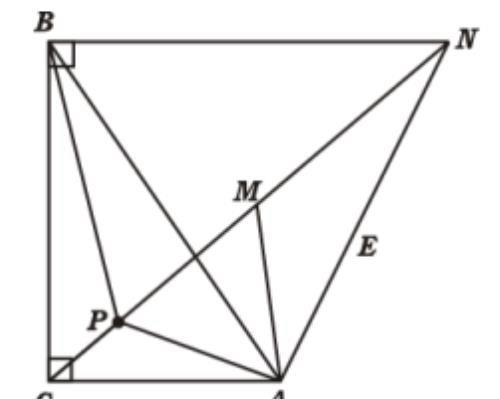
∴∠CBN=90°

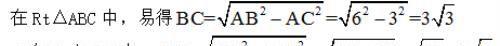
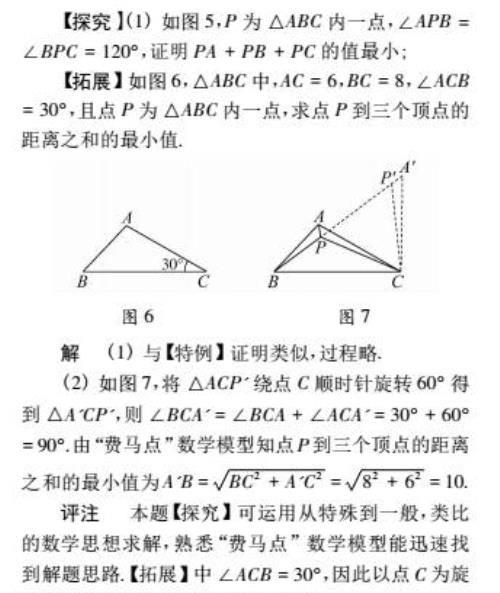
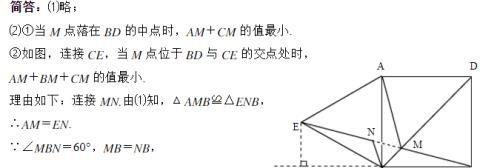
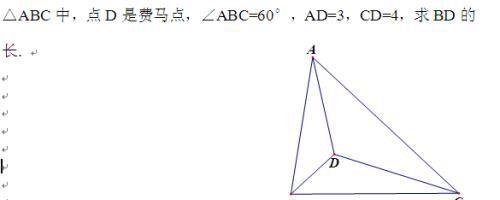
例4：

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！