矩阵和向量的乘法规则(矩阵和向量相乘的几何意义)

导语：线性代数专题5——矩阵和向量乘法的本质（中）

要搞清楚矩阵和向量乘法的本质，就必须要知道矩阵和向量乘法的意义。我们还是在坐标系中讨论。如图一，两个基向量i（1,0）和j（0,1）大家已经不陌生（什么是基向量，前面的专题已经讲过，大家可以翻看）。向量v的坐标是（1,2）,v=1i+2j=(1,0)+2(0,1)=(1,2)，这里的数字1和2还有一种非常重要的理解方式，表示将基向量i拉伸1倍（等于没有变化），将基向量j拉伸2倍；然后求和得到向量v。

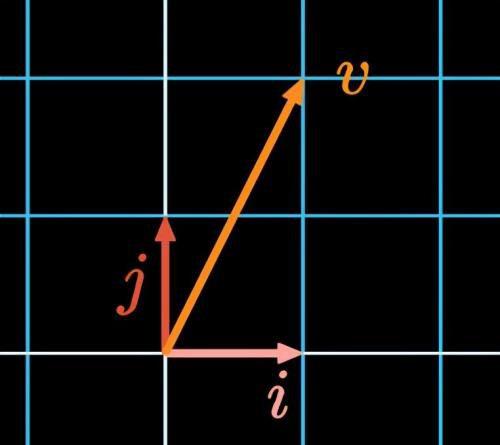
图一

可能大家会问这个有什么区别吗？有的，而且意义重大。可以思考一下，假设向量v=(3,5)，那么v=3i+5j。也就是说，向量v的坐标数字是标量，表示的是基向量的缩放倍数，那么如果改变了基向量，向量v就会随之发生改变。再假设两个基向量变成i=（1,1）和j（-1,1），v=3(1,1)+5(-1,1)=(-2,8)，注意向量的缩放倍数没有改变，改变的是基向量。这个内容理解了吗？这是线性代数中最重要的基础，有了这个基础，后面的问题就很容易了。

那么我们如何来简洁地描述上面的过程呢？这里需要知道一个向量（再次强调，此时向量的坐标数字表示基向量的缩放倍数），还需要知道两个改变后的基向量，于是我们将改变后的两个基向量写成两个列向量，构成一个2X2的矩阵，再规定用这个矩阵与原向量的乘法计算由于基向量改变所得到的新的向量。过程如图二。仔细理解这个过程，以后计算矩阵和向量乘法就不需要硬背计算公式了。

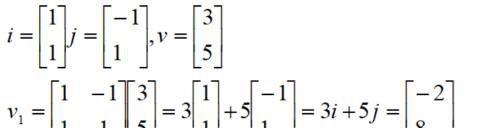
图二

下一篇，向大家展示矩阵与向量乘法在是如何与线性变换联系起来的。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小茹创作整理编辑！