数学的意义是什么(席南华院士数学的意义)

导语：这一数学意识，很大程度上决定了你和学霸之间的差距

我们的读书学习从小学到初中和高中，都需要学习数学，甚至进入大学，绝大部分专业都会把数学作为一门必修课或选修课，来培养大家的思维能力和综合能力。

虽然所有人都知道数学很重要，也很想学好它，但基于数学这门学科的特殊性，如系统性、逻辑性等都非常强，这给所有人的数学学习带来一定难度和挑战。因此，像如何学好数学？数学该怎么去学等类似的问题，成为很多老师、学生和家长非常关心的事情。

从粗浅的层面上来讲，学好数学无非就是先扎实掌握好基础知识和方法技巧，通过习题训练，提高运用知识解决问题的能力等等。看似这样的简单过程，很多人连最基本的知识定理都没有掌握好，却只会是迷恋题海战术，把数学学的又苦又累。

做事，解决问题，讲究方法技巧，数学学习亦是如此。从某个方面来说，中小学阶段的数学学习，我们可以从“数”与“形”两个角度去学习和研究，这就是常说的数形结合思想方法。如对于函数相关问题的解决，很多时候我们需要结合函数图象和性质，在图象中运用性质找到解决问题的关键，用性质定理去分析图象等。

数形结合思想一般是指从几何直观角度出发，利用几何图形的性质去研究数量之间的关系，从而找到代数问题的解决途径，或是利用数量关系来研究几何图形的性质，达到解决几何问题的一种数学思想方法。

简单地说数形结合思想方法，就是利用“数”与“形”之间的对应关系，实现数形结合，通过“数”与“形”的相互转化来达到解决数学问题的思想方法。

数形结合这一数学思想方法，不仅能帮助我们很好的去解决问题，更能培养和锻炼大家的逻辑思维能力和综合能力，提高数学素养等。

用数形结合思想解决问题，方法技巧讲解分析1：

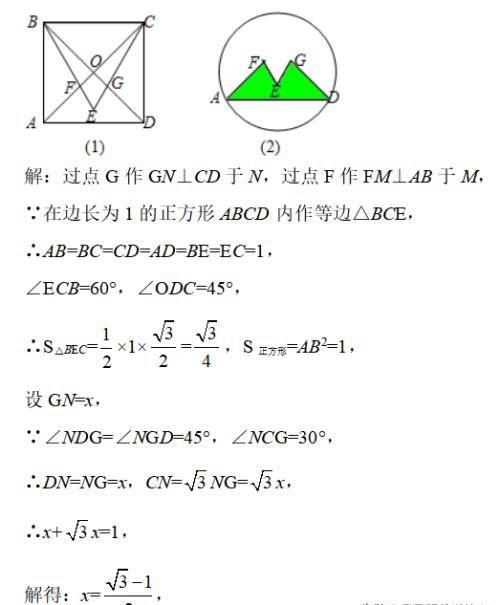
某校开展的一次动漫设计大赛，小明同学运用了数学知识进行了富有创意的图案设计，如图（1），他在边长为1的正方形ABCD内作等边△BCE，并与正方形的对角线交于点F、G，制作如图（2）的图标，请大家计算一下图案中阴影图形的面积．

考点分析：

正方形的性质；等边三角形的性质；解直角三角形。

题干分析：

首先过点G作GN⊥CD于N，过点F作FM⊥AB于M，由在边长为1的正方形ABCD内作等边△BCE，即可求得△BEC与正方形ABCD的面积，由直角三角形的性质，即可求得GN的长，即可求得△CDG的面积，同理即可求得△ABF的面积，又由S阴影=S正方形ABCD﹣S△ABF﹣S△BCE﹣S△CDG，即可求得阴影图形的面积．

解题反思：

此题考查了正方形，等边三角形，以及直角三角形的性质等知识．此题综合性较强，难度适中，解题的关键是注意方程思想与数形结合思想的应用。

数形结合思想的实质就是将抽象的数学语言与直观的图像结合起来，关键是要学会在代数问题与图形之间的进行相互转化。

用数形结合思想解决问题，方法技巧讲解分析2：

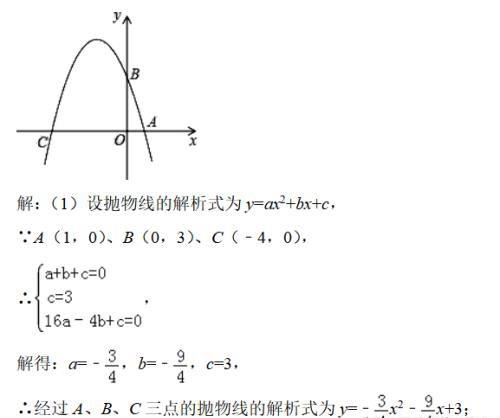
已知如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上上的三个点，且OA=1，OB=3，OC=4，

（1）求经过A、B、C三点的抛物线的解析式；

（2）在平面直角坐标系xOy中是否存在一点P，使得以以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；

（3）若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM﹣AM|的最大值时点M的坐标，并直接写出|PM﹣AM|的最大值．

题干分析：

（1）设抛物线的解析式为y=ax2+bx+c，把A，B，C三点坐标代入求出a，b，c的值，即可确定出所求抛物线解析式；

（2）在平面直角坐标系xOy中存在一点P，使得以点A、B、C、P为顶点的四边形为菱形，理由为：根据OA，OB，OC的长，利用勾股定理求出BC与AC的长相等，只有当BP与AC平行且相等时，四边形ACBP为菱形，可得出BP的长，由OB的长确定出P的纵坐标，确定出P坐标，当点P在第二、三象限时，以点A、B、C、P为顶点的四边形只能是平行四边形，不是菱形；

（3）利用待定系数法确定出直线PA解析式，当点M与点P、A不在同一直线上时，根据三角形的三边关系|PM﹣AM|＜PA，当点M与点P、A在同一直线上时，|PM﹣AM|=PA，

解题反思：

此题属于二次函数综合题，涉及的知识有：二次函数的性质，待定系数法确定抛物线解析式、一次函数解析式，菱形的判定，以及坐标与图形性质，熟练掌握待定系数法是解本题的关键。

数形结合思想方法虽然很强大，能帮助我们顺利解决问题，但在学习过程中，一定要注意这三件事：

一是要彻底明白一些概念和运算的几何意义以及函数图象的代数特征，对题目中的条件和结论既分析其几何意义又分析其代数意义；

二是恰当设未知数建立关系，由数思形，以形想数，做好数形转化；

三是准确的去确定未知数的取值范围。

用数形结合思想解决问题，方法技巧讲解分析3：

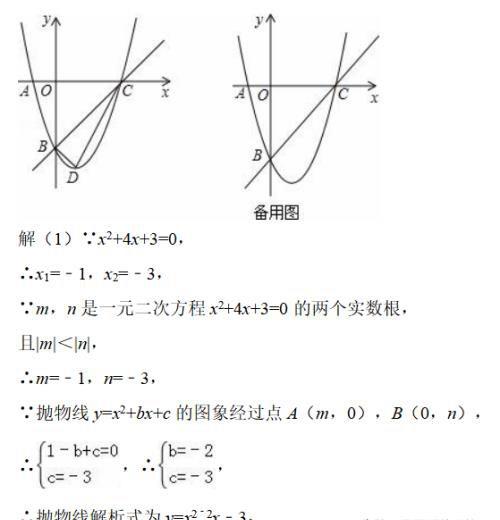
已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c的图象经过点A（m，0），B（0，n），如图所示．

（1）求这个抛物线的解析式；

（2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，试求出点C，D的坐标，并判断△BCD的形状；

（3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为√2个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

考点分析：

二次函数综合题．

题干分析：

（1）先解一元二次方程，然后用待定系数法求出抛物线解析式；

（2）先解方程求出抛物线与x轴的交点，再判断出△BOC和△BED都是等腰直角三角形，从而得到结论；

（3）先求出QF=1，再分两种情况，当点P在点M上方和下方，分别计算即可．

解题反思：

此题是二次函数综合题，主要考查了一元二次方程的解法，待定系数法求函数解析式，等腰直角三角形的性质和判定，解本题的关键是判定△BCD是直角三角形和数形结合思想的运用。

我们利用数形结合思想去解决问题，一个方面要学会把抽象的数学问题变得更加直观化和生动化，通过抽象思维和形象思维的相互转化，可以帮助我们认清数学问题的本质，优化解题方法，提高对数学的感悟等。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小珊创作整理编辑！