导数与函数的零点问题(三角函数的零点问题)

导语：函数的零点问题

1.函数的零点

对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点

2.方程，函数，函数图象之间的关系

方程f(x)=0有实数根函数y=f(x)的图象与X轴有交点函数y=f(x)与零点

3.函数零点的存在性定理

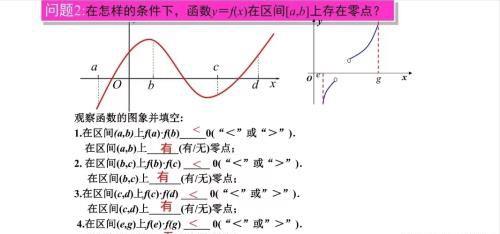
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线，并且有f(a)f(b)<0，那么，函数y=f(x)在区间（a,b）内有零点，即存在c∈（a,b），使得f(c)=0，这个c就是方程f(x)=0的根

注意：函数的零点不是一个点，零点指的是实数

例:

4．函数f（x）＝x+lnx﹣2零点所在区间为（　　）

A．（0，1） B．（e，） C．（1，e） D．（，1）

【分析】利用根的存在性定理进行判断区间端点处的符合即可．

【解答】解：因为f（1）＝1+ln1﹣2＝﹣1＜0，f（e）＝e+lne﹣2＝e﹣1＞0，

所以根据根的存在性定理可知在区间（1，e）内函数存在零点．

故选：C．

【点评】本题主要考查函数零点的判断，利用根的存在性定理是解决本题的关键．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小葵创作整理编辑！