从相位变化的角度理解小相位系统的特点(从相位变化的角度理解小相位系统的含义)

导语：从相位变化的角度理解最小相位系统

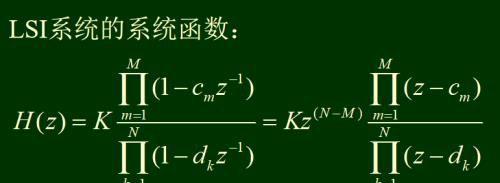
图a

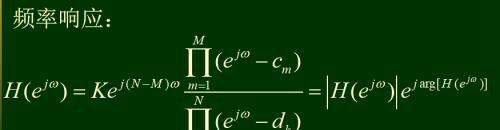
图b

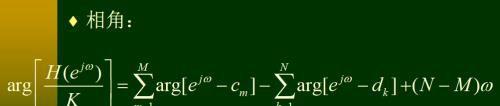
前面这几步都好理解。

图1

图2

图3

图1到图3是说，当w从0变到2pi时，单位圆内的零点或者极点向量都会变化2pi。

图1中，假设单位圆内的红圈点是一个零点，那么，由这个零点指向实轴Re[Z]的那个矢量就是一个零矢量

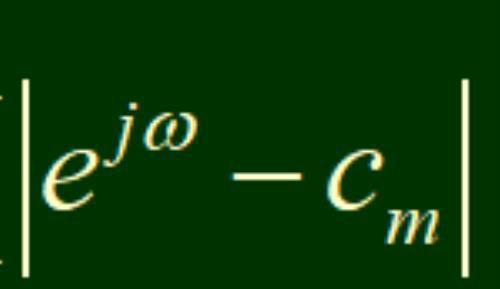
。这个零矢量绕单位圆旋转一周，其角度变化确实是2pi,因为仅仅考虑旋转角度的时候，矢量都可以平移，我们可以假设把刚才的那个零点移到原点，从而零矢量也平移到相应位置，再绕单位圆旋转一周，那么，其旋转的角度确实是2pi。

再考虑图1中单位圆外的那个零点，同样这个零点指向实轴Re[Z]的那个矢量就是一个零矢量。那为什么这个零矢量绕单位圆一周其变化的角度是0呢？还是可以从矢量平移的角度出发来考虑。我们可以假设把坐标的原点平移到单位圆外的那个零点处，但单位圆的位置不变，以保证这个零点处于单位圆外。这时候我们就可以看到，这个零矢量绕单位圆旋转一周后，其围绕原点旋转的角度确实是0。

上述结论同样适用于极点。

有了上述结论以后，再在相角的表达式中，

上面推论表明，图a中的系统函数，在w从0变到2pi的过程中，其旋转的角度与零极点的数目，以及在单位圆的外面还是里面是相关的。所以对于

从上面分析可以得出结论：

1：当全部零点和极点都在单位圆内的时候，系统函数的变化角度是0，这也是最小相位系统名称的由来。

2：当全部零点在单位圆外，而全部极点在单位圆内的时候（因果稳定系统），则称为最大相位系统。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小珊创作整理编辑！