高中数学三角函数知识点归纳总结(高中数学三角函数知识点总结及公式大全)
导语:高中数学:三角函数知识点
一、三角函数的概念
单位圆定义:设起点在原点的射线,与x轴正半轴形成一个角θ,并与单位圆(x2+y2=1)相交。这个交点的横坐标值和纵坐标值分别等于cosθ和sinθ。单位圆定义允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和 π/2弧度之间的角。逆时针方向的度量是正角,而顺时针的度量是负角,对于大于2π或小于-2π的角,可继续绕单位圆旋转得到。
如:角α的终边经过点P(3,-4),则cosα=3/5。
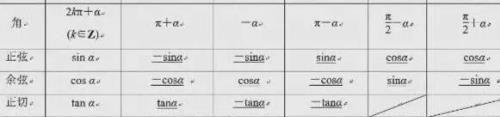
二、三角函数的诱导公式
任意角的三角函数均可与第一象限角的三角函数相互转化。(奇变偶不变,符号看象限)
诱导公式可以概括为:对于kπ/2±α(k∈Z)的三角函数值,当k是偶数时,得到α的同名函数值,即函数名不改变;当k是奇数时,得到α相应的余函数值sin→cos;cos→sin;tan→cot;cot→tan。(奇变偶不变),然后在前面加上把α看成锐角时原函数值的符号(符号看象限)。
如:sin(-2π-α)=sin(-4·π/2-α),k=-4为偶数,所以取sin;α看成锐角时,-2π-α在第四象限,sin(-2π-α)<0,符号为“-”。所以sin(-2π-α)=-sinα。
和差角公式正弦、余弦、正切、余切的和差角公式:
二倍角公式二倍角公式是利用和差角公式展开得到。
三、三角函数的图像
一个周期内的图像如下所示。
四、三角函数的值域
当x∈R时,sinx值域为[-1,1]。对于当x∈[a,b]时,求y=Asin(ωx+φ)的值域问题可用换元法,令t=ωx+φ,根据x的范围确定t的范围,然后再求出sint的范围,进而得到函数的值域。
如求函数y=4cos(x+π/6)-2,x∈[0,π/2]的值域,由x∈[0,π/2],得x+π/6∈[π/6,2π/3],即cos(x+π/6)∈[-1/2,√3/2],所以y∈[-4,2√3-2]。
五、三角函数的单调性
sinx的单调增区间是x∈[2kπ-π/2,2kπ+π/2],单调减区间是x∈[2kπ+π/2,2kπ+3π/2],k∈Z。cosx的单调增区间是x∈[2kπ-π,2kπ],单调减区间是x∈[2kπ,2kπ+π],k∈Z。求y=Asin(ωx+φ)的单调增区间,可把ωx+φ看作一个整体,即ωx+φ∈[2kπ-π/2,2kπ+π/2],k∈Z;解得x∈[(2kπ-π/2-φ)/ω,(2kπ+π/2-φ)/ω],k∈Z。
如f(x)=5sin(2x+π/4)的单调增区间为2x+π/4∈[2kπ-π/2,2kπ+π/2],k∈Z。则2x∈[2kπ-3π/4,2kπ+π/4],k∈Z。即x∈[kπ-3π/8,kπ+π/8],k∈Z。
六、三角函数的周期性
三角函数都有周期,最小正周期用T表示,nT(n为整数)也是该三角函数的周期。
sinx和cosx的最小正周期T=2π;tanx和cotx的最小正周期 T=π。y=Asin(ωx+B)+C或y=Acos(ωx+B)+C,其中A,ω,B,C为常数。周期只与x的系数ω有关,最小正周期T=2π/ω。
七、三角函数的对称性
正弦、余弦函数的图象既是中心对称图形,又是轴对称图形。正弦、余弦函数图像的对称轴是过函数图象的最高(低)点且垂直于x轴的直线;对称中心是图象与x轴的交点。
如:函数y=sinx图像关于直线x=kπ+π/2对称,关于点(kπ,0)中心对称。
八、三角函数图形变换
1.平移变换函数图像y=f(x)按向量(a,b)平移,得到的新图像按向量(-a,-b)平移可变回原图像,并满足原函数的对应法则,故新函数为:y-b=f(x-a)。即图形平移可视为函数按向量作减法(即“左加右减,上加下减”)。
如:将函数y=sinx图像往左平移5个单位,再往上平移3个单位后的函数为y-3=sin(x-(-5)),整理后:y=sin(x+5)+3。
2、放缩变换对函数y=f(x)图像x变化a倍、y变化b倍,得到的新图像x变化1/a倍、y变化1/b倍可变回原图像,并满足原函数的对应法则,新函数为:y/b=f(x/a)。
如:将函数y=sinx图像横坐标缩小5倍,得到函数y=sin5x,再将纵坐标放大3倍得到函数y/3=sin5x,整理后得y=3sin5x。
注意:平移变换和放缩变换均只对x与y进行变换。
如:由y=sinx得到y=5sin(2x+4)。
法1:先平移后放缩
先向左平移4个单位,然后横坐标变为原来的1/2,最后纵坐标伸长为原来5倍。
法2:先放缩后平移
先横坐标变为原来的1/2,然后向左平移2个单位(只对x变换,而不是2x),最后纵坐标伸长为原来5倍。
本文内容由快快网络小迪创作整理编辑!