不一样的余弦定理怎么求(余弦定理两种形式)

导语：不一样的余弦定理

不一样的余弦定理

余弦定理大家都学过，蛮简单的。即便没有学过也不打紧，一说你就会。

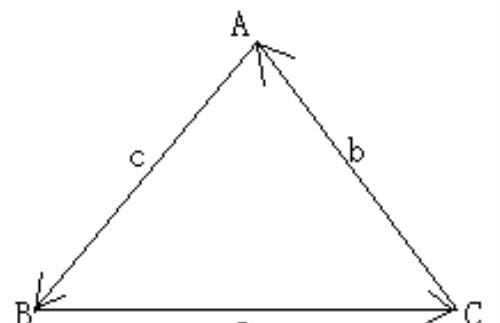
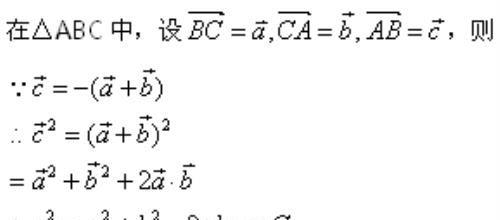
这就是余弦定理，其实质是首尾相连的一组向量之和为零，再将其平方得到。

那么，我们很容易同同样的手法将余弦定理推广到更广阔的空间。例如

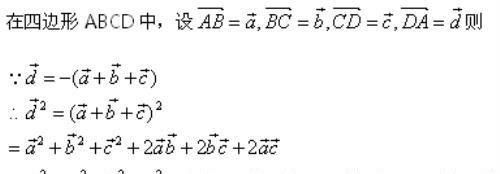
在四边形的余弦定理中，虽然看起来没有三角形的余弦定理漂亮，但它们的解法思路是一致的，都是将一边表示成其他边的向量和，然后平方。

如此继续，我们当然可以推导出任意n边形的余弦定理，不过这一点也不好玩。

我在玩余弦定理的时候，发现了两个比较好玩的结论。

例1、△ABC中，BC是最短边，在AB,AC边上取点E，D，使得BE=BC=CD则

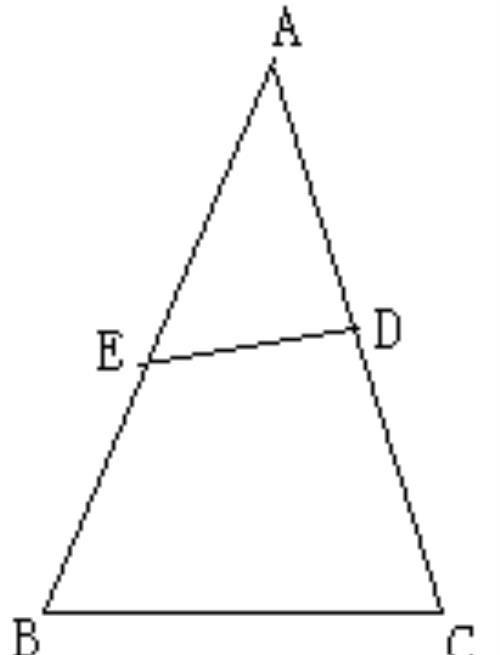
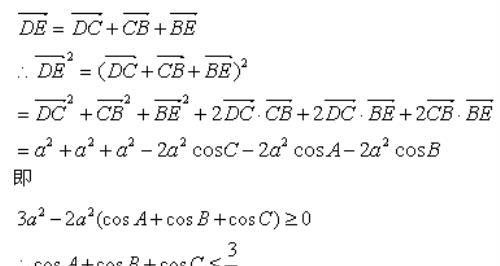
很有趣，由余弦定理出发，居然得到这么一个神奇的结论。

例2、对于正五边形ABCDE，设其边长为1，使用余弦定理可以发现

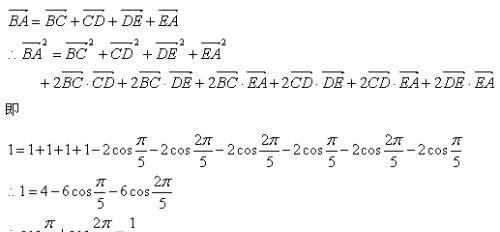
哈哈，居然得到了这样的结论，完全没想到。

亲爱的聪明的你，一定能挖掘出更多更有趣的结论。

譬如，四面体的余弦定理？

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小余创作整理编辑！