> 地理
皮克定理格点面积公式(格点多边形皮克定理)
导语:有趣的皮克定理——求格点四边形面积
皮克定理
皮克定理是奥地利数学家皮克发现的一个计算点阵中多边形的面积公式.皮克定理用于求格点多边形的面积。在信息时代,图像和信息均以数位或点阵方式给出,其特点为是均匀分布,不连续。这与连续情形下的传统欧式几何有明显的不同,也为分析带来了障碍。皮克定理在传统欧式几何与近代数位几何之间建立了联系。
格点多边形
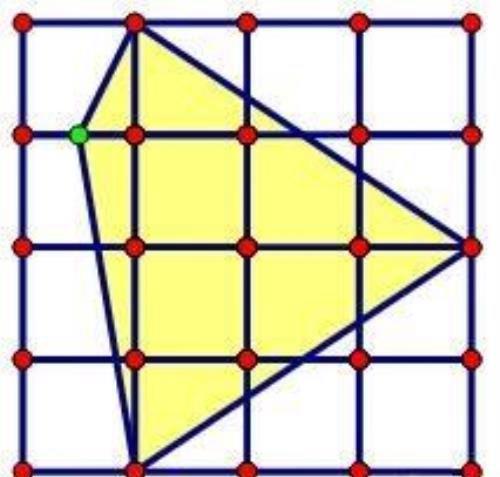
如下图,每个小正方形的边长是1,图中小正方形的顶点称为“格点”,如果一个多边形的每个顶点都在格点上,则称该多边形为“格点多边形”,下图是一个格点四边形。
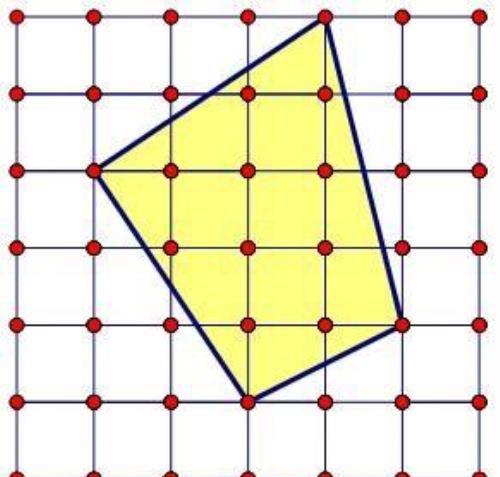
格点多边形面积计算
小学数学课上,用加减法来计算格点多边形的面积,下图是常用方法。
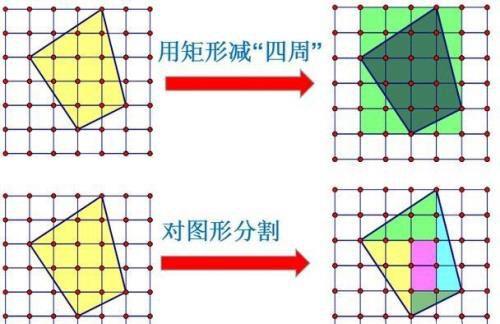
如果多边形过于复杂,比如下图,用加减法计算就有些复杂了,有没有简单的方法呢?
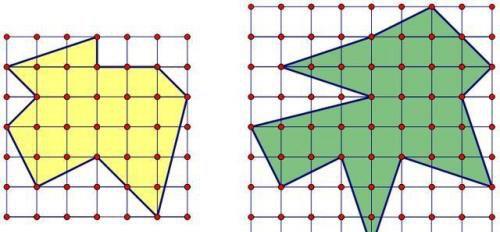
皮克定理
1899年,奥地利数学家乔治·亚历山大·皮克给出了格点多边形的计算公式:

(其中n表示多边形内部的点数,s表示多边形边界上的点数,S表示多边形的面积)
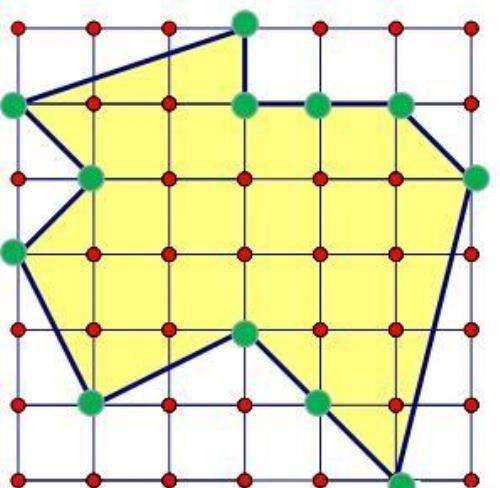
如上图中的多边形τ的面积,用皮克定理计算为:
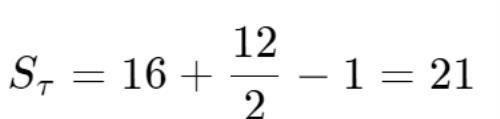
皮克定理不适用的类型
1非格点多边形,即多边形某个顶点不在格点上,如下图
2有“洞”的图形,即图形内部被挖去了一部分的,如下图,这个面积用两次皮克定理才可求出。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小葵创作整理编辑!