地球引力势能公式推导(地球引力势能计算方法)

导语：地球的引力势能公式及其应用

引力势能公式的推导

处在地球引力场中的物体在靠近地球或远离地球时，万有引力会对物体做功，从而引起物体引力势能的变化，且引力做多少功，物体的引力势能就会减小多少-----功能关系。

如图所示，设地球的质量为M，物体的质量为m，物体与地球之间的距离为r。现将物体从r处移到离地球无穷远处，地球引力对物体做了多少功呢？

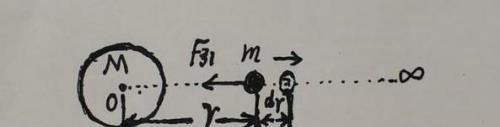
当物体移动很小的距离dr时，万有引力对物体做的功dW为:

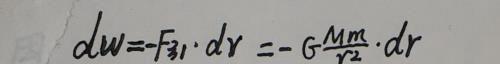
将这些功累积起来，就可得到地球引力对物体做的功W为:

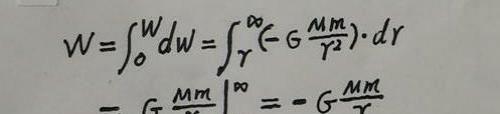
规定物体在无穷远处的引力势能为零，即Ep∞=0，结合功能关系可以的到:

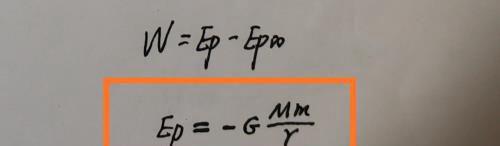
以上即为物体在距离地球r的地方引力势能的表达式。

引力势能公式的应用

1.推导发射航天器的第二宇宙速度

当航天器的发射速度超过一定值时，它就可以摆脱地球引力的束缚，飞离地球进入环绕太阳运行的轨道。这个脱离地球引力的最小发射速度就是第二宇宙速度。

设地球的半径为R，当航天器的发射速度为v时，航天器恰好能脱离地球的吸引，即到达（相对地球）无穷远处。该过程航天器的发射动能转化为引力势能，根据机械能守恒定律得:

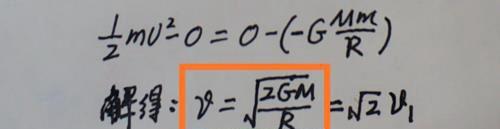
从以上结果可以看出，第二宇宙速度是第一宇宙速度的根2倍，约等于11.2km/s。

2.计算卫星变轨的机械能变化

如图所示为卫星变轨的简单示意图，我们知道，卫星从一个低轨道1‘’升迁‘’至高轨道3至少要经过两次点火加速，所以卫星运行的轨道越高，机械能越大。卫星在变轨过程中至少要补充多少机械能呢？

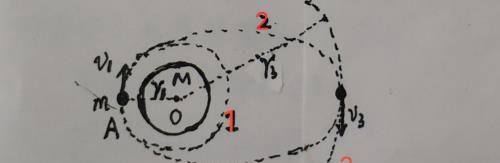
卫星在轨道1和轨道3上做圆周运动时，都是由万有引力提供向心力，根据牛顿第二定律可确定卫星在两个轨道上运行时的动能如下：

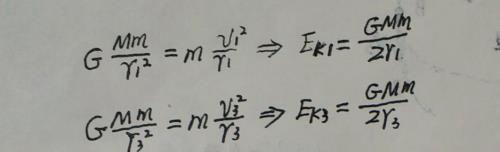
结合引力势能公式可确定卫星在两个轨道上运行时的机械能分别为：

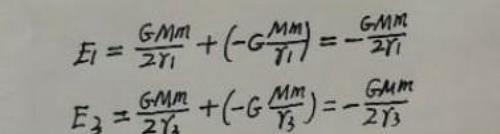
所以卫星在变轨过程中至少要补充的机械能为：

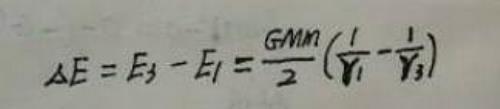
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小鸣创作整理编辑！