导语：有趣的等效转化，数学解题中的金钥匙

问题引入

　平面上有n条直线两两相交，但没有三条直线交于一点。问这n条直线把平面划分成多少个区域？

分析：当我们遇到一个较为复杂的数学问题时，往往想起与它类似的问题，类似的形式，类似的解法等等，并联想起与它相应的定理，相应的公式，相应的法则等，从而把所遇到的问题与联想起的问题进行比较。通过类比推理的思考方法，将所遇到的问题进行等效，向想起的问题，又将联想起的类似的方法到所遇到的问题上。因此在解决直线分平面的问题时，我们可通过类比和联想，从点分直线的情况出发来探索直线分平面的问题。

解：首先我们来考虑点分直线的问题。设一直线上的n个点能将直线分成an个部分，那么容易得到an=n+1。

接着我们再来研究直线分平面问题。平面上有n条直线，其中任何两条不平行，任何三条不共点，设这n条直线将平面分成bn个部分，在观察的基础上进行归纳可知，第k＋1条直线与前k条直线均相交得k个交点，由前面点分直线的情形可知，该直线被k个交点分成k＋1段，而其中每一段都把平面上的每一个区域分成两个区域，所以平面部分应增加(k＋1)块。由此可得递推关系式为

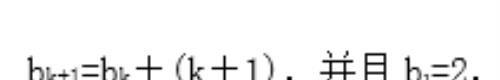
　　所以，当k=1时，b₂-b₁=2，

　　当k=2时，b₃-b₂=3，

　　当k=3时，b₄-b₃=4，

　　…

　　当k=n-1时，bn-bn-1=n，

　　把以上n-1个式子相加得：

　　(b₂-b₁)＋(b₃-b₂)+(b₄-b₃)＋…＋(bn-bn-1)

　　＝2＋3＋4＋…＋n，

　　则： bn-b₁=2＋3＋4＋…＋n，

　　即：bn=2＋2＋3＋4＋…＋n。

　　

　　因此n条两两相交，且没有三线交于一点的直线可把平面分成

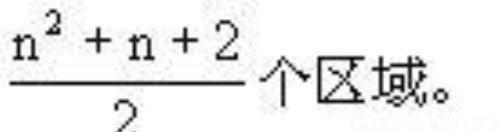
问题反思

本题还可利用差分法来帮助发现规律，从而解决问题，首先我们考虑一条直线、两条直线、三条直线，……，将平面所分的区域数。

　　计算数列2，4，7，11，…的差分

　　由于二阶差分数列是非零的常数列，所以猜测bn是n的2次多项式bn=an2＋bn＋c，利用待定系数法，进一步求出a、b、c的值。

　　

　　

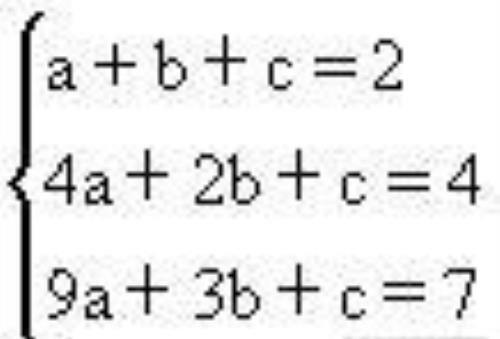
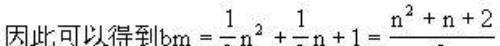
　但我们运用差分法猜测得到的结论，还需通过数学归纳法加以论证。

方法应用

1．阅读资料：阅读材料，完成任务：

材料阿尔•花拉子密（约780～约850），著名数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”．

他用以下方法求得一元二次方程x²+2x﹣35＝0的解：

将边长为x的正方形和边长为1的正方形，外加两个长方形，长为x，宽为1，拼合在一起的面积是x²+2×x×1+1×1，而由x²+2x﹣35＝0变形得x²+2x+1＝35+1（如图所示），即右边边长为x+1的正方形面积为36．所以（x+1）²＝36，则x＝5．

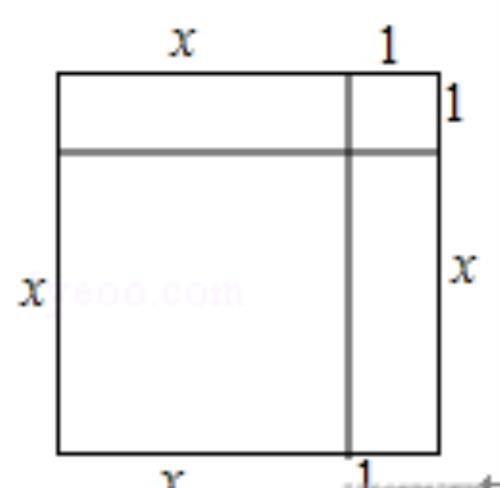
任务：请回答下列问题

（1）上述求解过程中所用的方法是　 　．

A．直接开平方法 B．公式法 C．配方法 D．因式分解法

（2）所用的数学思想方法是　 　的．

A．分类讨论思想 B．数形结合思想 C．转化思想 D．公理化思想

（3）运用上述方法构造出符合方程x2+8x﹣9＝0的一个正根的正方形．

【解答】（1）由材料可知，题中运用的方法是配方法，故答案为C；

（2）根据材料可知，运用的数学思想是数形结合的思想，故答案为B；

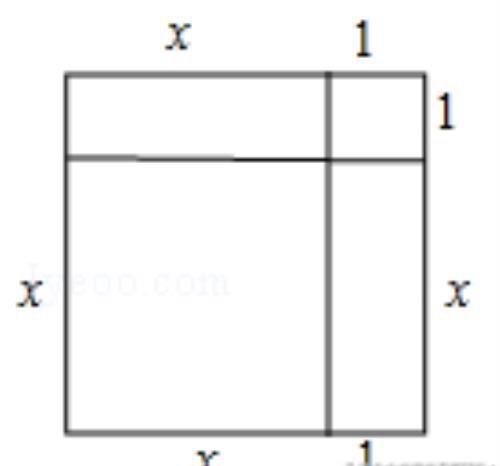
（3）x²+8x﹣9＝x²+8x+16＝16+9＝25，∴（x+4）2＝25，∴x＝1；

如图所示：

2．阅读思考：我们思考解决一个数学问题，如果从某一角度用某种方法难以奏效时，不妨换一个角度去观察思考，换一种方法去处理，这样有可能使问题“迎刃而解”．

问题解决：

（1）上述解题过程中，用到的数学学习中常用的思想方法是（　　）

A、类比思想 B、函数思想 C、转化思想 D、整体思想

【解答】（1）将高次方程转化为一元一次方程和一元二次方程得出是转化思想；故选：C；

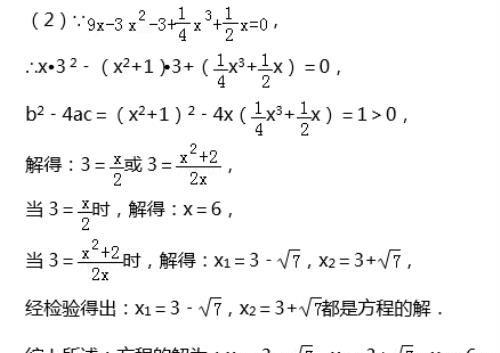
3．阅读下列材料，按要求回答问题．

（1）观察下面两块三角尺，它们有一个共同的性质：∠A＝2∠B，我们由此出发来进行思考．

在图（1）中作斜边上的高CD，由于∠B＝30°，可知c＝2b，∠ACD＝30°，于是AD＝b/2，BD＝c﹣b/2，由于△CDB∽△ACB，可知，即a²＝c•BD．同理b2＝c•AD，于是a²﹣b²＝c（BD﹣AD）＝c（c﹣b）＝bc．对于图（2），由勾股定理有a²＝b²+c²，由于b＝c，故也有a²﹣b²＝bc．

在△ABC中，如果一个内角等于另一个内角的2倍，我们称这样的三角形为倍角三角形，两块三角尺都是特殊的倍角三角形，对于任意倍角三角形，上面的结论仍然成立吗？我们暂时把设想作为一种猜测：

如图（3），在△ABC中，若∠CAB＝2∠ABC，则a²﹣b²＝bc．

在上述由三角尺的性质到“猜测”这一认识过程中，用到了下列四种数学思想方法中的哪一种选出一个正确的并将其序号填在括号内（　　）

①分类的思想方法②转化的思想方法③由特殊到一般的思想方法④数形结合的思想方法

（2）这个猜测是否正确，请证明．

【解答】（1）③正确．

（2）a²﹣b²＝b•c仍正确.

证明：延长CA到D，使AD＝AB＝c,

∴∠BAC＝∠D+∠ABD＝2∠D,

∵∠BAC＝2∠ABC,∴∠D＝∠ABC,∴△ABC∽△BDC,

方法总结

在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化，进而达到解决的一种方法。将复杂问题通过变换转化为简单问题;将难解的问题通过变换转化为容易求解的问题；将未解决的问题通过变换转化为已解决的问题。

探索是人类思维中最活泼、最生动、最富有魅力的活动，探索过程是一个不断提出设想，验证设想，修正和发展设想的过程。本题采用的类比法也是探索问题的一种重要方法。尤其是联想与类比交织在一起的共同探索与发现，在解决问题时，如果我们能根据数学知识的特点，运用类比、联想的方法积极思考，从已有的知识来探索新的知识，既有利于认知结构的完善，又有利于探索能力的培养。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小竹创作整理编辑！