斯坦纳—莱默斯定理简单证法(莱莫斯斯坦纳定理)

导语：世界难题——斯坦纳——莱黙斯定理的证明

如图1，设△ABC的∠A、∠B、∠C的对边分别为a、b、c，AD是△ABC的角平分线，AD的长与三角形的三边a、b、c的关系如何呢？

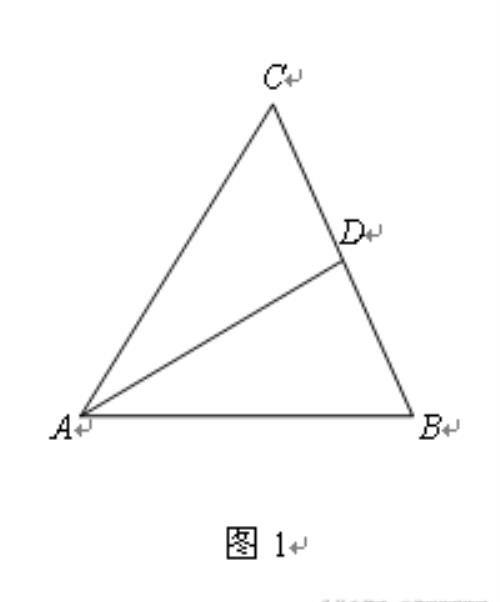
如图2，作△ABC外接圆，延长AD交外接圆于E，连接BE．则

AD·DE=BD·DC，∠E=∠C，

因为AD平分∠BAC，

所以∠BAE=∠CAD，

所以△ABE∽△ADC，

所以AB/AD=AE/AC，

即c/AD=(AD+DE)/b，

由AD·DE=BD·DC，得

DE=BD·DC/AD，

所以c/AD=(AD+ BD·DC/AD)/b，

整理，得AD2=bc-BD·DC.

由三角形角平分线性质定理，得

BD/DC=AB/AC=c/b，

所以BD/(a-BD)=c/b，

整理，得BD=ac/(b+c)，

所以DC=a-BD=a-ac/(b+c)=ab/(b+c)．

所以AD2=bc- ac/(b+c)× ab/(b+c)

=bc/(b+c)2·[(b+c)2-a2]，

所以AD=√bc[(b+c)2-a2]/(b+c).

这就是△ABC的∠A平分线长公式，

记作LA=√bc[(b+c)2-a2]/(b+c).

同理，LB=√ca[(c+a)2-b2] /(c+a) ·，

LC=√ab[(a+b)2-c2] 1/(a+b) .

从角平分线从公式可见，当a=b时，显然有

LA=√bc[(b+c)2-b2]1/(b+c) ，

LB=√bc[(c+b)2-b2] /(c+b) ，

所以LA= LB.

这就是大家所熟悉的“等腰三角形底角平分线相等”，该命题早在二千多年前欧几里得的《几何原本》中就已作为定理．但对于它的逆命题——“角平分线相等的三角形是等腰三角形”在《几何原本》中却是只字未提，一直到1840年，莱默斯（C.L.Lehmus）在他给斯图姆（C.Sturm）的信中提出请求给出一个纯几何证明．但斯图姆未能解决，就向许多数学家提出这一问题．首先给出证明的是瑞士几何学家斯坦纳（J.Steiner,1796—1863），因而这一定理就称为斯坦纳-莱默斯定理．

对于斯坦纳-莱默斯定理的证明大多采用的反证法，下面我们运用三角形角平分线长公式给予证明．

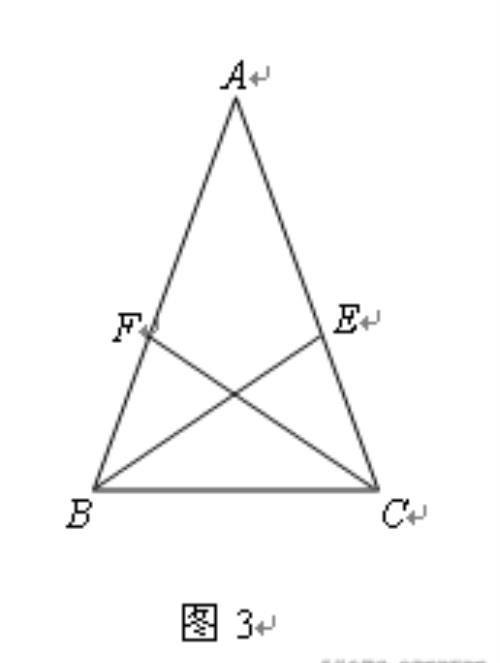
如图3，△ABC中，BE、CF是角平分线，且BE=CF．求证：AB=AC．

证明：设∠A、∠B、∠C的对边分别为a、b、c，则由三角形角平分线长公式，得

BE=√ca[(c+a)2-b2]/(c+a) ，

CF=√ab[(a+b)2-c2]/(a+b)，

因为BE=CF，

所以√ca[(c+a)2-b2]/(c+a)= √ab[(a+b)2-c2]/(a+b) ，

两边平方，并整理，得

ac·(a+b+c)(a+c-b) /(a+c)2=ab ·(a+b+c)(a+b-c) /(a+b)2，

两边除以a(a+b+c)，得：c·(a+c-b) /(a+c)2 =b ·(a+b-c) /(a+b)2，

去分母，得c(a+b)2(a+c-b)=b(a+c)2(a+b-c)，

设b-c=x，则c-b=-x，所以

c(a+b)2(a-x)=b(a+c)2(a+x)，

整理，得：ac(a+b)2-cx(a+b)2=ab(a+c)2+bx(a+c)2，

再整理为：bx(a+c)2+ cx(a+b)2= ac(a+b)2- ab(a+c)2，

所以[b(a+c)2+ c(a+b)2]x=a(a2c+2abc+b2c-a2b-2abc-bc2)，

即[b(a+c)2+ c(a+b)2]x=a[(a2c-a2b)+(b2c-bc2)]

= a[a2(c-b)+bc(b-c)]

=a(-a2x+bcx)=ax(bc-a2)，

即[b(a+c)2+ c(a+b)2]x=ax(bc-a2)，

所以[b(a+c)2+ c(a+b)2-a(bc-a2]x=0，

易知[b(a+c)2+ c(a+b)2-a(bc-a2]≠0，

所以x=0，

所以b-c=0，b=c，

所以AB=AC．.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小舻创作整理编辑！