铅垂法求面积公式是什么(什么叫铅垂法求面积)
导语:「中考专题复习」铅垂法求面积最值问题探究

专题导入
导例:抛物线y=交x轴正半轴于点A(3,0),交y轴于点B(0,3),且这个抛物线的顶点为C.连接AB、AC、BC,则抛物线的对称轴为直线 ,线段CD的长为 ,△ABC的面积为 .
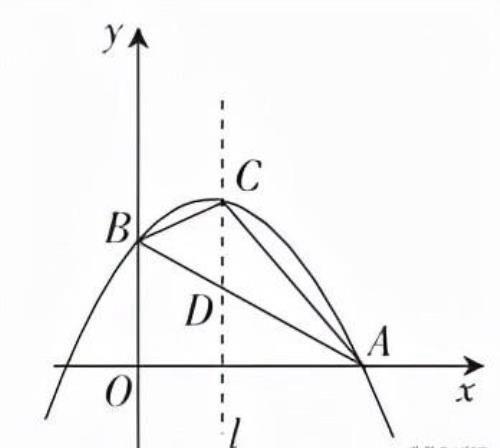
导例答案:x= 2 3.
方法点睛
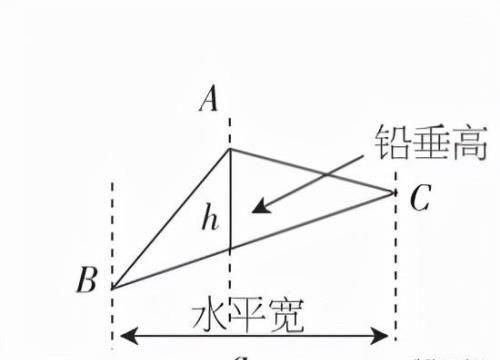
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”,我们可得出一种计算三角形面积的另一种方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.
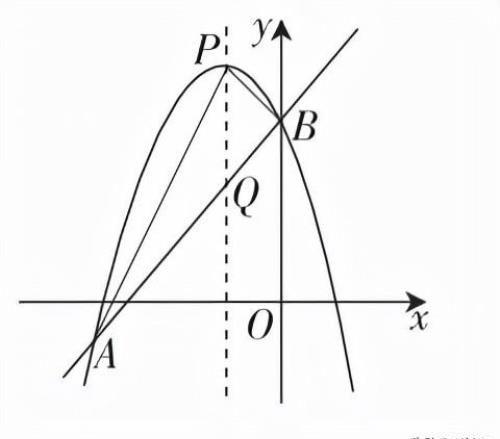
根据上述方法,我们来得到求三角形的面积的最值问题的方法:S△PAB=·PQ·,根据二次函数解析式设出点P的坐标,结合一次函数解析式从而得到点Q的坐标,从而转化为S与点P横坐标之间的二次函数解析式,再根据二次函数增减性求最值.一般情况下,当铅垂线段PQ最大时,S△PAB取得最大值.
典例精讲
类型一:抛物线上动点产生的三角形面积的最值
例1 在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的解析式;
(2)如图,连接DC,D

B,设△BCD的面积为S,求S的最大值.
【分析】(1)根据题意得到B、C两点的坐标,
设抛物线的解析式为y=(x-4)(x-m),将点C的坐标代入求得m的值即可;(2)过点D作DF⊥x轴,交BC与点F,设D(x,x2-x-2),则DF=-x2+2x,然后列出S与x的关系式,最后利用配方法求得其最大值即可.
类型二:抛物线上动点产生的四边形的面积
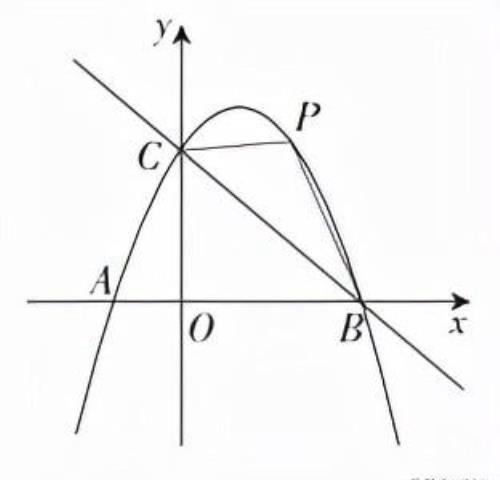
例2. 如图,抛物线y=ax2+bx-3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为直线x=-1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).
(1)直接写出抛物线的解析式;
(2)探究:当动点N在对称轴l上时,是否存在PB⊥NB,且PB=NB的关系,若存在,请求出此时点P的坐标,若不不存,请说明理由;
(3)是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值,若不存在,请说明理由.

【分析】(1)由对称轴可求得B点坐标,结合A、B两点坐标,利用待定系数法可求得抛物线解析式;(2)过点P作PM⊥x轴于点M,设抛物线对称轴l交x轴于点Q.可证明△BPM≌△NBQ,则可求得PM=BQ,可求得P点的纵坐标,利用抛物线解析式可求得P点坐标;(3)连接AC,设出P点坐标,则可表示出四边形PBAC的面积,再利用二次函数的性质可求得其最大值.
专题过关
1.如图,抛物线y=ax2+bx+c与坐标轴交点分别为A(﹣1,0),B(3,0),C(0,2),作直线BC.
(1)求抛物线的解析式;
(2)点P为抛物线上第一象限内一动点,过点P作PD⊥x轴于点D,设点P的横坐标为t(0<t<3),求△ABP的面积S与t的函数关系式.
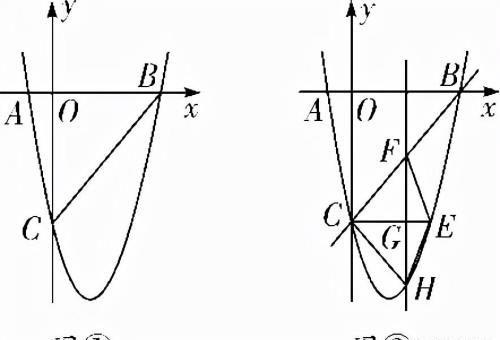
2.如图①,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数解析式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标;
(3)如图②,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积.
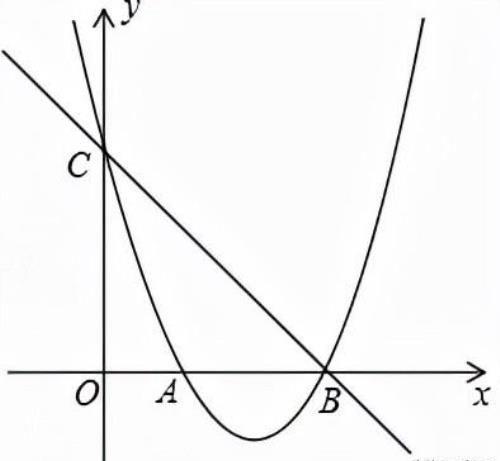
3.如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.
(1)求这个二次函数的解析式;
(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;
(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.
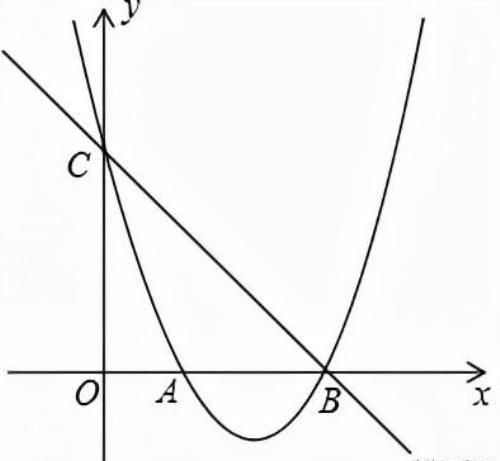
备用图
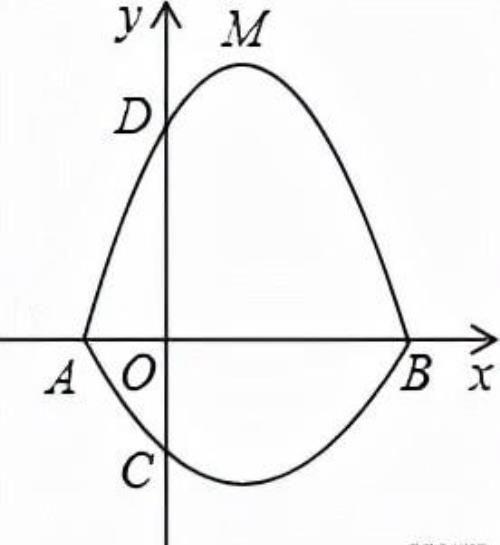
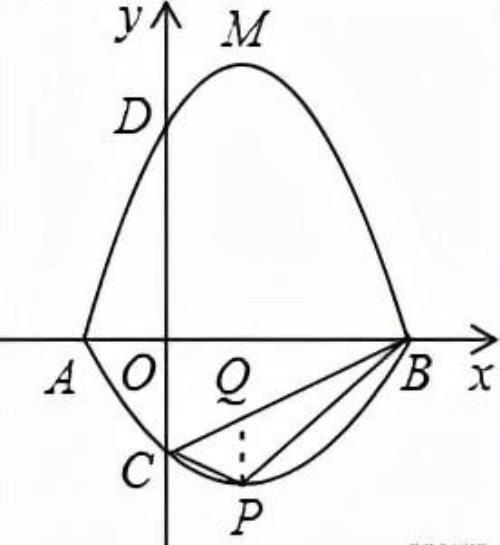
4.如图,在平面直角坐标系中,A,B为x轴上两点,C,D为y轴上的两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A,B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.
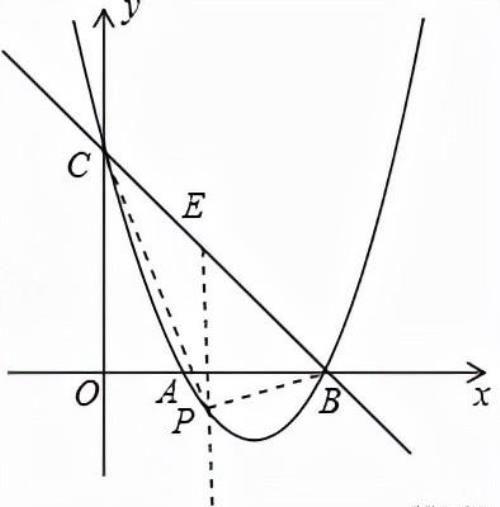
5.已知直线y=x+2分别交x轴、y轴于A,B两点,抛物线y=x2+mx﹣2经过点A,和x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;
(3)如图2,经过点M(﹣4

,1)的直线交抛物线于点P,Q,连接CP,CQ分别交y轴于点E,F,求OE•OF的值.

专题一:二次函数中的三角形面积最值问题 答案
例1 (1)把x=0代y=x﹣2得y=﹣2,∴C(0,﹣2).
把y=0代y=x﹣2得x=4,∴B(4,0).
设抛物线的解析式为y=(x﹣4)(x﹣m),将C(0,﹣2)代入,得2m=﹣2.
解得m=﹣1.∴A(﹣1,0).
∴抛物线的解析式y=(x﹣4)(x+1),即y=x2﹣x﹣2.
(2)如图所示:过点D作DF⊥x轴,交BC与点F.
设D(x,x2-x-2),则F(x,x-2),DF=(x-2)-(x2-x-2)=-x2+2x.∴S△BCD=OB•DF=×4×(-x2+2x)=-x2+4x=-(x2-4x+4-4)=-(x-2)2+4.∴当x=2时,S有最大值,最大值为4.此时点Q为线段AB的中点.

例2.(1)y=x2+2x-3;∵A(1,0),对称轴L为直线x=-1,
∴B(-3,0),将AB两点坐标代入得,
∴,解得∴抛物线的解析式为y=x2+2x-3.
(2)如解图①,过点P作PM⊥x轴于点M,连接BP,过点B作BN⊥PB交直线L于点N,
设抛物线的对称轴与x轴交于点Q,
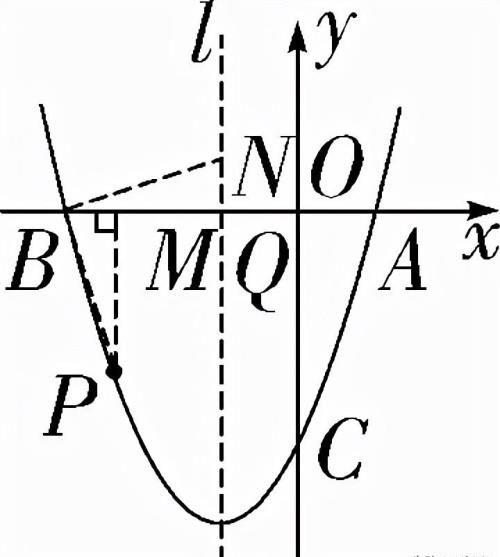
第6题解图①∵PB⊥NB,∴∠PBN=90°,∴∠PBM+∠NBQ=90°.
∵∠PMB=90°,∴∠PBM+∠BPM=90°.∴∠BPM=∠NBQ.又∵PB=NB,
∴△BPM≌△NBQ.∴PM=BQ.由(1)得y=x2+2x-3,∴Q(-1,0),B(-3,0)
∴BQ=2,∴PM=BQ=2.
∵点P是抛物线y=x2+2x-3上B、C之间的一个动点,且点P的纵坐标为-2,
将y=-2代入y=x2+2x-3,得-2=x2+2x-3,
解得x1=-1-,x2=-1+ (不合题意,舍去) .∴点P的坐标为(-1-,-2);
(3)存在.如解图②,连接AC,BC,CP,PB,过点P作PD∥y轴交BC于点D,
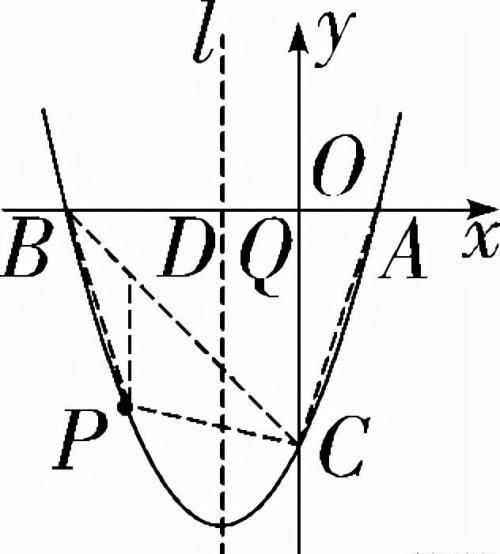
图②
∵A(1,0),B(-3,0),C(0,-3),∴S△ABC=×3×4=6.
直线BC的解析式为y=-x-3.
设P(t,t2+2t-3),则D(t,-t-3),
∴S△BPC=×3×(-t-3-t 2-2 t +3)=-t2-t,
∴S四边形PBAC=-t2-t+6=- (t+)2+,
当t=-时,S四边形PBAC存在最大值,最大值为.此时点P的坐标为(-,-).
专题过关
2.(1)把A(﹣1,0),B(3,0),C(0,2)代入y=ax2+bx+c,得
解得a=﹣,b=,c=2.∴抛物线的解析式为y=﹣x2+x+2.
(2)设点P的坐标为(t,﹣t2+t+2).∵A(﹣1,0),B(3,0),∴AB=4.
∴S=AB•PD=×4×(﹣t2+t+2)=﹣t2+t+4(0<t<3).
3.(1)∵抛物线过点A(-1,0)和点B(5,0),
∴∴, ∴抛物线的函数解析式为y=x2-4x-5;
(2)∵OB=OC=5,∴∠ABC=∠OCB=45°.
∴以B,C,D三点为顶点的三角形要与△ABC相似,必须要有一个角等于45°.
(ⅰ)当点D在点C的下方时,∠BCD=180°-45°=135°,
∴不会出现45°角,∴此种情况不存在;
(ⅱ)当点D在点C的上方时,∠BCD=45°,易得BC=OB=5,AB=OA+OB=1+5=6,
存在两种情况:①当△BCD∽△ABC时,,
即=.∴CD=,OD=CD-OC=-5=.∴D(0,);
②当△DCB∽△ABC时,=,即=.∴CD=6,OD=CD-OC=6-5=1.
∴点D(0,1) .
综上所述,点D的坐标为(0,1)或(0,)时,以B,C,D为顶点的三角形与△ABC相似;
(3)由y=x2-4x-5,当y=-5时,x2-4x-5=-5,解得x1=0,x2=4.
∴E(4,-5) .∴CE=4.
设H(a,a2-4a-5) .∵点H是在直线CE下方抛物线上的动点,
∴0<a<4.设直线BC的解析式为y=kx+b,
把点B(5,0),C(0,-5)代入得
解得∴直线BC的解析式为y=x-5.
设点F(a,a-5),∴FH=a-5-(a2-4a-5)=-a2+5a.
∵CE⊥FH,∴S四边形CHEF=CE·FH=-2a2+10a=-2(a-)2+.
∵0<a<4,∴当a=时,四边形CHEF面积有最大值,最大值是,此时H(,-).
4.(1)将A(1,0)
,B(3,0)代入函数解析式,得
解得∴这个二次函数的解析式为y=x2-4x+3;
(2)当x=0时,y=3,即点C(0,3).
设BC的解析式为y=kx+b,将点B(3,0)点C(0,3)代入函数解析式,得
解这个方程组,得
∴直线BC的解析是为y=﹣x+3.
过点P作PE∥y轴,设交直线BC于点E坐标为(t,﹣t+3).
∴PE=﹣t+3﹣(t﹣4t+3)=﹣t2+3t.∴S△BCP=S△BPE+SCPE=(﹣t2+3t)×3=﹣(t﹣)2+.
∵﹣<0,∴当t=时,S△BCP最大=.
(3)设M(m,﹣m+3),N(m,m2﹣4m+3).
∴MN=m2﹣3m,BM=|m﹣3|.
当MN=BM时,①m2﹣3m=(m﹣3),解得m=.
②m2﹣3m=﹣(m﹣3),解得m=﹣.当BN=MN时,∠NBM=∠BMN=45°.
m2﹣4m+3=0,解得m=1或m=3(舍去);
当BM=BN时,∠BMN=∠BNM=45°,﹣(m2﹣4m+3)=﹣m+3,解得m=2或m=3(舍去);
当△BMN是等腰三角形时,m的值为,﹣,1,2.
5.(1)y=mx2﹣2mx﹣3m=m(x﹣3)(x+1),∵m≠0,∴当y=0时,x1=﹣1,x2=3.
∴A(﹣1,0),B(3,0);
(2)设C1:y=ax2+bx+c,将A,B,C三点的坐标代入得:
解得故C1:y=x2﹣x﹣.
如图:过点P作PQ∥y轴,交BC于Q.
由B、C的坐标可得直线BC的解析式为:y=x﹣,
设P(x,x2﹣x﹣),则Q(x,x﹣),PQ=x﹣﹣(x2﹣x﹣)=﹣x2+x,
S△PBC=PQ•OB=×(﹣x2+x)×3=﹣(x﹣)2+,
当x=时,S△PBC有最大值,Smax=.此时y=×()2﹣﹣=﹣,∴P(,﹣);
(3)y=mx2﹣2mx﹣3m=m(x﹣1)2﹣4m,
顶点M坐标(1,﹣4m),当x=0时,y=﹣3m.∴D(0,﹣3m),B(3,0).
∴DM2=(0﹣1)2+(﹣3m+4m)2=m2+1,
MB2=(3﹣1)2+(0+4m)2=16m2+4,
BD2=(3﹣0)2+(0+3m)2=9m2+9.
当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.
①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,
解
得m=﹣1(∵m<0,∴m=1舍去);
②DM2+MB2=BD2时有:m2+1+16m2+4=19m2+9,
解得m=﹣(m=舍去).
综上,m=﹣1或﹣时,△BDM为直角三角形.

1.(1)把y=0代入y=x+2得:0=x+2,解得:x=﹣4,∴A(﹣4,0).
把点A的坐标代入y=x2+mx﹣2得:m=,∴抛物线的解析式为y=x2+x﹣2.
(2)过点D作DH∥y轴,交AB于点H,
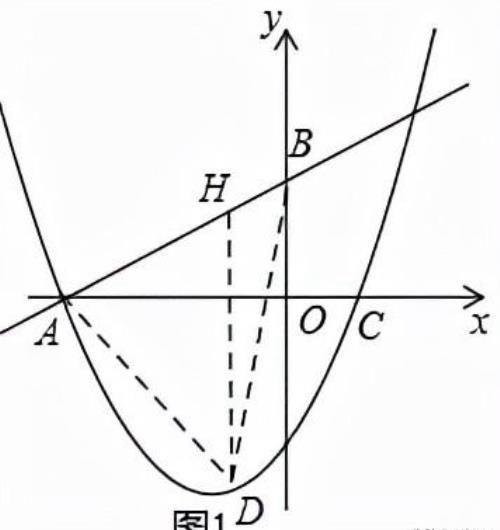
设D(n,n2+n﹣2),H(n,n+2).∴DH=(n+2)﹣(n2+n﹣2)=﹣(n+1)2+.
∴当n=﹣1时,DH最大,最大值为,此时△ABD面积最大,最大值为××4=9.
(3)把y=0代入 y=x2+x﹣2,得:x2+3x﹣4=0,解得x=1或x=﹣4.∴C(1,0).
设直线CQ的解析式为y=ax-a,CP的解析式为y=bx-b.则解得或∴xQ=2a-4.同理xP=2b-4.
设直线PQ的解析式为y=kx+b,把M(﹣4,1)代入得:y=kx+4k+1.
∴.∴x2+(3﹣2k)x﹣8k﹣6=0.
∴xQ+xP=2a﹣4+2b﹣4=2k﹣3,xQ•xP=(2a﹣4)(2b﹣4)=﹣8k﹣6.
解得ab=﹣.又∵OE=﹣b,OF=a,∴OE•OF=﹣ab=.
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小冰创作整理编辑!