导语：启发式搜索的一般性理解和思考－搜索算法系列

上篇文章谈到的Dijkstra算法属于一种启发式的算法。因为，Dijkstra算法非盲目遍历所有路径，找出最短路径。而是，在算法过程中，引入"节点和路径的关系变化"的思想启发，使得算法时间复杂度和空间复杂度得到优化。

试想，没有绝对盲目的搜索算法，一切搜索算法都是启发式的。因为，即使遍历所有的可能性，那么，也至少需要拥有判断目标是否为待寻找答案的先验知识或启发知识。因此，对于前面提到的"假币问题"，"4皇后问题"，以及"Dijkstra问题"都属于启发式搜索。本篇文章，引入爬山法，最陡爬山法等，从"启发式搜索"这一角度，进一步来抽象和固化对搜索算法的一般性理解。

第三十八篇　启发式算法的一般性理解和思考－搜索算法系列

回到"假币问题"

假币问题的"背景时空"

是"一枚枚拥有一定质量的硬币，其中有一个假币，假币和其他质量不同"

假币问题的-"问题时空"

是用天平一次次的称重，最终通过称重确认假币。这一次次的称重仿佛构成了我们最终找到假币的过程，不妨称之为"假币路径"。而，找到假币的称重方案有很多，即有很多假币路径。众多的"假币路径"构成假币问题的"问题时空"。

搜索算法是围绕着的"问题时空"进行的，比如，假币问题的算法最终得到的是一个找到最终假币的称重序列，这个称重序列归属于问题时空；

搜索算法的"局部形"

这里"局部形"概念即为对"背景时空"的采样方式，这取决于我们对问题时空的"启发思路"，是我们算法的核心和关键。

比如，假币问题，可以采用４个一组称重，或８个一组称重，或２个一组称重。也可先想办法识别出真币的质量，再一个个称重，最终识别出质量有偏差的假币。因此，这个对背景时空进行数据采样的格式，我们称之为搜索算法的"局部形"，即搜索的节点。

搜索算法的"整体形"

搜索算法的"整体形"由"局部形"所呈现，是对"局部形"的广度搜索和深度搜索。整体形，也取决于我们对问题时空的"启发思路"，也是我们算法的核心和关键。

比如：对于假币问题，我们以８个一组进行称重，这属于广度搜索。一旦我们发现称重偏差，说明假币出现了。我们再针对一组进行拆分称重，逐步锁定假币，这属于深度搜索。

搜索算法的"开闭集"

开闭集依赖于"搜索算法"的"局部形"。比如：我们若采用８个一组的称重方式时。这时，如果天平两端的16枚硬币质量平衡，我们可以把这两组硬币，扔进闭集。而对于开集，就是剩下硬币所形成的８个一组的组集合。

搜索算法的"运动机制"

"运动机制"对应着算法的广度搜索和深度搜索。在程序设计上体现为"队列"和"栈"。我们容易理解，对于"队列"的先进先出操作，呈现的是先来后到，逐个覆盖，广度遍历得搜索运动。而"栈"的先进后出操作，呈现的是先进后出，承前启后，深度探索的搜索运动。

假币问题的"启发思想"

基于上述概念的梳理和总结，我们思考，在搜索算法中需要面对的是，第一，如何从背景时空中提取和定义"局部型"；第二，广度搜索何时终止，深度搜索何时结束。这决定了我们怎么收敛到答案路径。即如何判断局部形或路径就是答案。

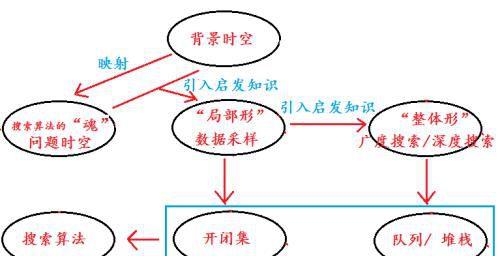
如上图，们此时应该有如下归纳理解：

启发思想引入以问题时空为前提；

局部形（具体节点）的定义可引入启发思想；

整体形（搜索策略）的执行可引入启发思想

爬山法

背景时空-爬山法

背景时空为高低起伏的群山。

问题时空-爬山法

是爬山者试图爬到最高点，但爬山者并不知道最高点在哪，于是爬山者朝着比当前位置更高的点的方向前行。

启发思路-爬山法

爬山法局部形（搜索节点）的定义，即比爬山者当前位置高的节点；

爬山法整体形（搜索策略）采用的是，朴素简单的策略，即选择比当前位置更高的节点，不断迭代走下去，走出一条折线。

最陡爬山法

我们来看下最陡爬山法描述，即"从多个比当前状态"更好的节点"中做出一个选择。而不仅仅是选择向比当前状态"更好"（更高）的目标移动"。

其实，我们理解。

爬山法和最陡爬山法区别在于在局部形的定义中引入的启发思想不同；而，在整体形策略方面引入的启发思想并无差别，即一门心思走下去，不回头。

最佳优先搜索

爬山法是一种短视的算法，最陡爬坡法比爬山法引入的启发思想更理性一些。但，二者思路均是在"局部形"的定义上引入启发思想，而在"整体形"上没有任何启发思想的引入，可以理解为"只进不退"，一旦选错，会永远错下去。他们在遇到山麓问题，高原问题以及山脊问题时，束手无策。

如果我们在"整体形"上引入启发思想，那么，我们相信，我们的算法会更智能。而"最佳优先搜索算法"便是这样的一种算法。

最佳优先搜索维持开放节点列表的优先级队列。优先级队列里存放的未探索的节点。因此，最佳优先搜索，可以找到全局最优的答案。

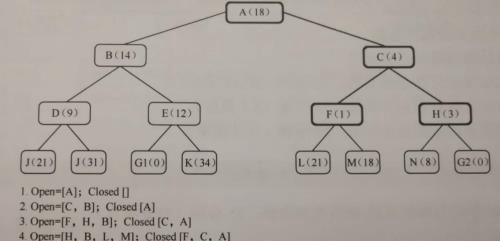
总结

启发思想是搜索算法的"魂"；

这个"魂"存在于两处地方，一个地方是"局部形"的定义，即解决如何从背景时空中提取和定义"局部型"的问题，即"搜索的节点"；另一个地方是"整体形"的呈现，是解决 广度搜索和深度搜索何时终止以及如何判断局部形或路径就是答案的问题，即"搜索的策略"；

我们可以理解，爬山法和最陡爬山法的精华只在于"局部形"。而最佳优先搜索，不仅在于"局部形"，还在于知进退，具有全局视野，比爬山法能找到更优的答案。当然，也消耗更多的空间和算力。

这里，我们再抽象理解，什么是算法？算法的本质是人对外界时空的认知（即，知识，规律，数学）。认知体现在两方面，一是对局部物质的抽象和定义（即局部型），二是局部的抽象和定义在全局下的关系和变化（即整体形）。然后，把这种局部和整体的认知用计算机语言表达，并在计算机中模拟运行，达到进一步认知和理解外界时空，以及预测外界时空未来的目的。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！