导语：简明的反向传播算法推导

反向传播算法是深度学习的训练基础，但其推导是个难点。本文以多层感知机为例，尝试较为简明地推导反向传播算法。

多层感知机的基本结构如下图所示：

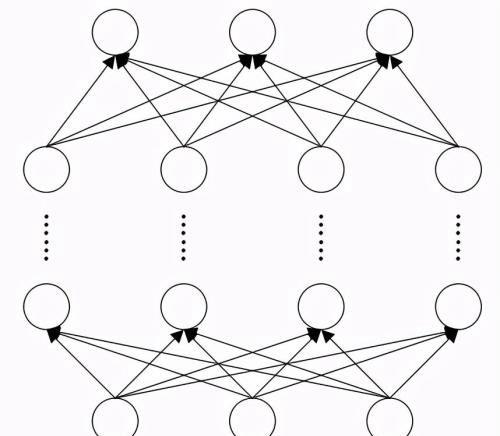
多层感知机的基本结构

前向传播过程

我们设网络有层，其中第层的输入为，输出为。在每一层中首先用输入、权重和偏置计算变换，然后经过激活函数得到，计算损失函数。注意网络的权重为矩阵，偏置、输入均为向量。

反向传播

反向传播算法基于梯度下降策略，以目标的负梯度方向对网络的参数进行更新。给定损失函数和学习率，反向传播的基本形式为：

上式的核心为求损失对参数的梯度，根据链式求导法则，可得：

对再用链式求导法则：

在前向传播时，是从第层传到第层，但反向传播时梯度是从第层传到第层，因此才有式（2）中的链式求导。令，看作损失函数在第层产生的残差量，同理可得，带入式（2）可得：

结合式（2）和式（3），式（1）可写为：

损失函数对偏置的梯度可以用同样的方法求得。最后，得到反向传播的参数更新公式：

大家可以自己尝试推导一下偏置的梯度，看看为何少了个~

反向传播算法就推导到这里啦，这是最基本的形式，但万变不离其宗，不论什么样的神经网络，都可以通过链式求导法则推导出其具体的参数更新公式。如果对你有帮助的话，求关注点赞转发~如果有什么问题，欢迎留言~

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小凡创作整理编辑！