中考数学要想考得好此类题型少不了怎么办(中考数学题难吗)
导语:中考数学要想考得好,此类题型少不了

如何拿下中考数学的高分,我们讲的最多,研究的最频繁,除了做好基础知识的复习工作之外,就是要学会拿下压轴题的分数。
一名考生,如果能顺利解决压轴题,拿到相应的分数,而且把这种解题准确率维持在较高的水平,那么这名考生的中考数学成绩一定不会低。
为什么这么说呢?
要想正确解决压轴题,首先你的基础知识必须要过关,扎实掌握好每一个知识点,熟练运用每一个知识点;其次,对相应的方法技巧必须要非常熟悉,能够较好的运用这些方法技巧去顺利解决问题;最后,对数学思想方法有一定的了解,并且能够熟练运用它们去分析问题和解决问题等等。
因此,对于很多学生来说,再冲刺压轴题之前,应先把知识定理、方法技巧、数学思想方法等扎实掌握好,努力提高运用能力,这样你在面对压轴题的时候,才会有足够的底气去冲刺解决。
压轴题的难,不仅体现在知识综合性方面,更体现在题型的复杂层面上。如分类讨论问题,粗略的划分有函数相关的分类讨论,也有几何相关的分类讨论,更有函数与几何相结合的分类讨论问题等。

中考必考热点压轴题,分类讨论讲解分析1:
已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD.BC于点E.F,垂足为O.
(1)如图1,连接AF.CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P.Q分别从A.C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A.C.P.Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P.Q的运动路程分别为a.b(单位:cm,ab≠0),已知A.C.P.Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.




考点分析:
矩形的性质;全等三角形的判定与性质;线段垂直平分线的性质;勾股定理;平行四边形的判定与性质;菱形的判定与性质.
题干分析:
(1)先证明四边形AFCE为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;根据勾股定理即可求得AF的长;
(2)①分情况讨论可知,当P点在BF上.Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;②分三种情况讨论可知a与b满足的数量关系式.
解题反思:
本题综合性较强,考查了矩形的性质.菱形的判定与性质.勾股定理.平行四边形的判定与性质,注意分类思想的应用.
什么是分类讨论?
分类讨论思想是指当被研究的问题存在一些不确定的因素,无法用统一的方法或结论给出统一的表述时,按可能出现的所有情况来分别讨论,得出各种情况下相应的结论,分类讨论思想有利于学会完整地考虑问题,化整为零地解决问题。

中考必考热点压轴题,分类讨论讲解分析2:
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1) 设点P的纵坐标为p,写出p随变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于32/25的k值?若存在,请求出符合的k值;若不存在,请说明理由。


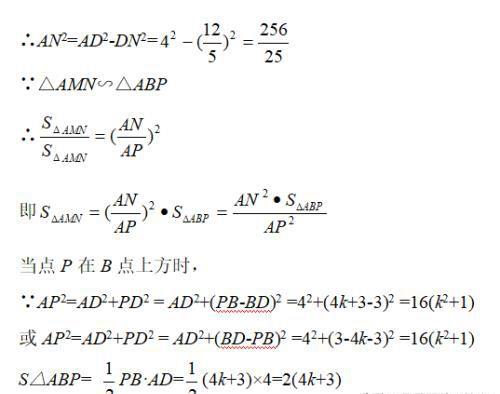

考点分析:
相似三角形的判定与性质;一次函数综合题;勾股定理;圆周角定理;切线的性质;代数几何综合题。
题干分析:
(1)由切线的性质知∠AOB=∠OAD=∠ADB=90°,所以可以判定四边形OADB是矩形;根据⊙O的半径是2求得直径AD=4,从而求得点P的坐标,将其代入直线方程y=kx+3即可知p变化的函数关系式;
(2)连接DN.∵直径所对的圆周角是直角,∴∠AND=90°,∴根据图示易证∠AND=∠ABD;然后根据同弧所对的圆周角相等推知∠ADN=∠AMN,再由等量代换可知∠ABD=∠AMN;最后利用相似三角形的判定定理AA证明△AMN∽△ABP;
(3)存在.把x=0代入y=kx+3得y=3,即OA=BD=3,然后由勾股定理求得AB=5;又由相似三角形的相似比推知相似三角形的面积比.分两种情况进行讨论:①当点P在B点上方时,由相似三角形的面积比得到k2﹣4k﹣2=0,解关于k的一元二次方程;②当点P在B点下方时,由相似三角形的面积比得到k2+1=﹣(4k+3),解关于k的一元二次方程.
解题反思:
本题主要考查了梯形的性质,矩形的判定,相似三角形的判定和性质以及一次函数的综合应用,要注意的是(3)中,要根据P点的不同位置进行分类求解.

不同类型的分类讨论问题,分类标准和顺序可能存在一定的区别,方法多种多样,一般情况下遵循以下分类的原则:
1、分类中的每一部分是相互独立的;
2、一次分类按一个标准;
3、分类讨论应逐级进行;
4、正确的分类必须是周全的,既不重复、也不遗漏。
很多时候一些学生无法用分类讨论的方法去解决问题,主要是在面对问题的时候,不知从何下手,特别是要分类不重不漏,对于很多学生来说,存在着一定困难了。
中考必考热点压轴题,分类讨论讲解分析3:
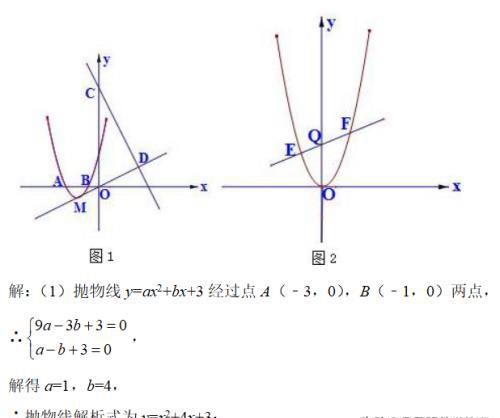
如图1,抛物线y=ax2+bx+3经过点A(﹣3,0),B(﹣1,0)两点,
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=﹣2x+9与y轴交于点C,与直线OM交于点D,现将抛物线平移,保持顶点在直线OD上,若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图2,将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E.F两点,问在y轴的负半轴上是否存在一点P,使△PEF的内心在y轴上,若存在,求出点P的坐标;若不存在,说明理由.



考点分析:
二次函数综合题。
题干分析:
(1)根据抛物线y=ax2+bx+3经过点A(﹣3,0),B(﹣1,0)两点,代入解析式求出即可;
(2)由(1)配方得y=(x+2)2﹣1,利用函数平移①当抛物线经过点C时,②当抛物线与直线CD只有一个公共点时,分别分析求出;
(3)由点E.F的坐标分别为(m,m2),(n,n2),得出m+n=km•n=﹣3,利用作点E关于y轴的对称点R(﹣m,m2),作直线FR交y轴于点P,
由对称性知∠EFP=∠FPQ,此时△PEF的内心在y轴上,求出即可.
解题反思:
此题主要考查了二次函数的综合应用以及三角形内心的特点,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合以及分类讨论是这部分考查的重点也是难点同学们应重点掌握。
分类讨论相关题型作为中考数学的热点和重点,也是我们在中考复习过程中经常遇到的难点所在。
分类讨论思想的数学问题具有明显的逻辑性、综合性、探索性,能训练人的思维条理性和概括性和缜密性,它对学生的基本知识和基本技能等都提出了更高的要求。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑!