模拟退火算法的改进(模拟退火算法如何产生新解)

导语：采用模拟退火算法改进悬索结构找形

采用通用有限元结构分析软件进行悬索结构找形是一个经典的问题，比如这样一个典型案例：

在水平跨距L=120m，纵向高差h=20m的两端有一悬索，悬索截面积为：

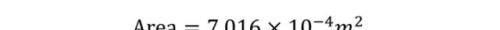
单位长度的重量为γ=65N，弹性模量为：

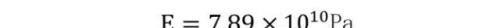
求悬索在水平张力为9000N时的悬索形状和对应悬索的原始长度。

一般情况下主要的分析流程是：

1. 在弦长位置建立初始几何模型。

2. 给定一个很小的初始应变。

3. 计算此时在重力作用下的响应。

4. 判断此时的水平张力的大小。

5. 如果此时的水平张力的大小大于给定的水平张力，则根据误差的大小，人为将模型更新比例系数设置成几个档。

6. 重复计算步骤3～6，直到水平张力小于给定的水平张力，或是达到给定的误差允许范围。

7. 后处理得到原始悬索的长度。

通过上述流程，基本可以完成悬索的找形。但是在找形过程中存在以下问题：

1. 在循环迭代过程中，人为给定的误差范围，有时可能造成迭代找形发生跳跃。即在某次迭代过程中误差大于迭代收敛误差，当更新模型后，误差小于迭代收敛相对误差，但相对误差（绝对值）又大于迭代收敛相对误差。从而错过了有效解，进而在后续的迭代过程中没法返回，导致出现死循环。

2. 在循环过程中，实际参与的变量数目有相对误差控制数值，模型更新比例系数。因此，要人为给定多档合理的数值往往需要多次尝试，甚至，即使多次尝试也不能得到较好的结果。另外，当设定好每个档的数值以后，当原始参数改变时，又需要重新调整。

为了解决上述问题，采用模拟退火算法，即模型更新的比例系数随着相对误差的大小变化。当相对误差较给定相对误差大时，取模型更新系数为1，当相对误差小于给定相对误差的相反数时，采用退火算法，并构建相对误差与模型更新系数的函数：

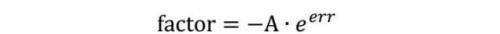
其中：factor为模型更新比例系数，A为待定系数，err为相对误差值

这样人为需要调整的参数就只有待定系数A。这里的负号确保了即使再迭代的时候错过了有效解，也可以退回去，确保迭代的有效进行。

也可根据输出文件，绘制误差和水平张力随迭代次数的曲线。

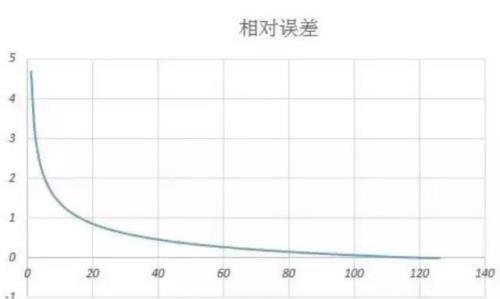
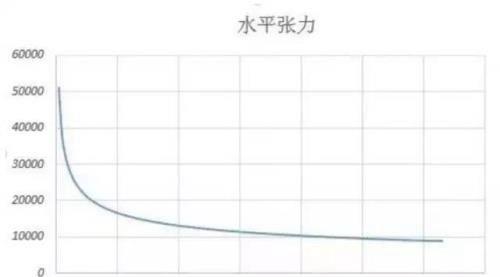
由以上2个曲线可知，随着迭代的进行，相对误差和水平张力急剧下降，从而减少了迭代的次数。

另外模拟退火算法本质是一种贪婪算法，收敛的精度与快慢与给定的模型更新比例系数关系非常大。当采用定值更新系数时，更新比例系数越小时，其收敛的精度越高，但是收敛越慢；当更新的比例系数越大时，其收敛精度越低，同时有可能因为过大，导致错过了有效解，而陷入死循环；在设置时需要综合考虑。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！