二次函数应用题经典例题及答案(二次函数应用题及答案所有题型)

导语：二次函数应用题常考的5大题型，网友说：这些题都是中考中的常客

应用二次函数模型解决生活应用型问题，是提高数学素质的训练内容之一，充分体现了数学基本方法的灵活运用和基本数学思想的渗透。在中考中，以下这4个题型属于高频考题。

求几何图形的最大面积问题是二次函数应用题的重点题型，这类题一般有这样的特征：面积随着某条线段长的变化而变化。在解这类题时，先根据题意列出面积与线段长的函数关系式；再根据函数的性质求最大值。

在实际生活中，利用二次函数性质求一个物体的最大高度。这类题出现在考试中时，一要会用配方法把一般式化为顶点式；二要注意自变量的取值范围。特别注意当二次函数的顶点坐标不在自变量的取值范围之内时，需要根据这段函数图象的增减行来确定最大值或最小值。

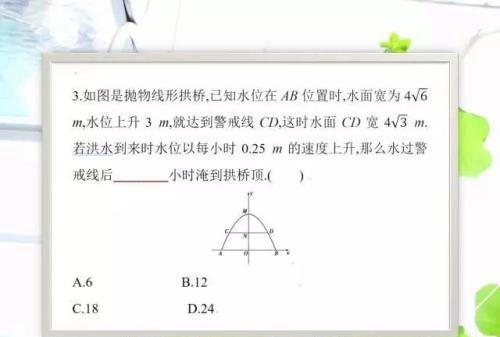
生活中的拱形桥问题，需要转化讲其抽象成一个数学模型。在解这类题时，当碰到没有直角坐标系，需要先建立直角坐标系，转化为二次函数来解决问题。解题技巧：一般把抛物线的顶点作为坐标系的原点建立平面直角坐标系，用待定系数法求二次函数的表达式。

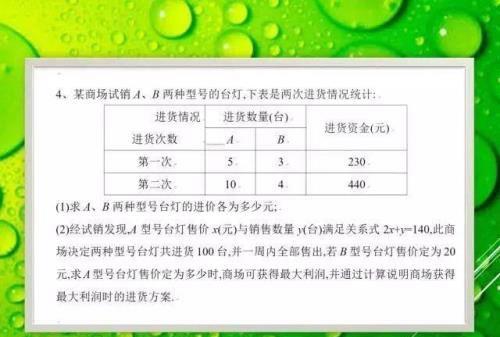
利用二次函数解决实际生活中的利润问题，应认清变量所表示的实际意义，注意隐含条件的使用，同时考虑问题要全面。利用二次函数解决最大利润问题的一般步骤：先运用“总利润=总售价-总成本”或“总利润=每件商品所获利润×销售数量”，建立利润与价格之间的二次函数关系式，求出这个函数关系式的顶点坐标，即求得最大利润。

不等式与函数综合应用题是每年中考中常考的应用题，不等式主要体现了自变量的取值范围。

利用二次函数解决实际生活问题的一般方法及几何图形的最值问题，解这类题需要注意：（1）分析问题中的变量、常量，以及它们之间的关系，设出变量；（2）用函数解析式表示它们之间的关系（建立数学模型）；（3）借助二次函数的解析式、图象和性质等求解实际问题；（4）检验结果，得出符合实际意义的结论。

​

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小茹创作整理编辑！