基本不等式求值有关问题的方法是什么(基本不等式求值有关问题的方法是)

导语：基本不等式求最值有关问题的方法

利用基本不等式求最值有关问题的关键是凑出“和”或“积”为定值，并保证等号成立，常见的方法技巧如下:

(1)拆(裂项拆项):对分子的次数不低于分母次数的分式进行整式分离→分离成整式与“真分式”的积，再根据分式中分母情况对整式进行拆项，为应用基本不等式凑定值创造条件；

(2)并(分组并项):目的是分组后各组可以单独应用基本不等式，或分组后先对一组应用基本不等式，再在组与组之间应用基本不等式得出最值；

(3)配(配式配系数，凑出定值):有时为了挖掘出“积”或“和”为定值，常常需要根据题设条件釆取合理配式、配系数的方法，使配式与待求式相乘后可以应用基本不等式得出定值，或配以恰当的系数后，使积式中的各项之和为定值；

(4)换（常值代换、变量代换）:对条件变形，以进行“1”的代换，从而构造利用基本不等式求最值的形式，常用于“已知ax+by=m(a，b，x，y均为正数，求1/x+1/y的最小值”和“已知a/ⅹ+b/y=m（a，b，ⅹ，y均为正数），求x+y的最小值”两种类型。

例:

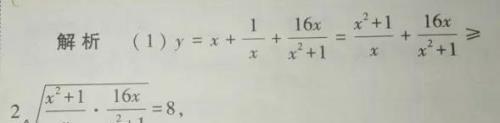
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！