证明切线垂直于过切点的半径(证明切线需要什么条件)

导语：此题要证明切线并求弦长，解题难点是垂径定理及相似三角形的运用

各位朋友，大家好！近来一段时间，数学世界将持续为大家分享初中数学题，希望笔者的分析与讲解能够为广大初中生学好数学提供一些帮助！今天，数学世界分享一道有关圆的证明题和解答题，涉及圆的知识，切线的判定，等腰三角形的判定和性质，相似三角形的判定和性质等知识。

一直以来，数学世界都是精心选择一些数学题分享给大家，目的是希望由此激发学生们对数学这门课程的兴趣，并能给广大学生的学习提供一点帮助！接下来，数学世界就与大家一起来看题目吧！

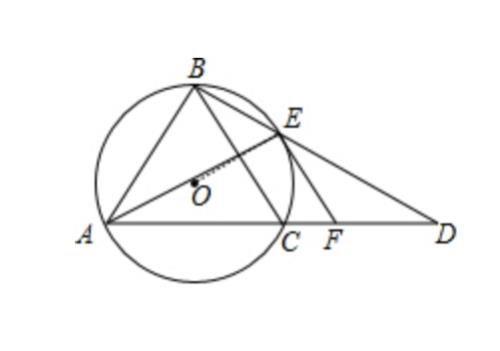
例题：（初中数学综合题）如图，已知⊙O是△ABC的外接圆，AB=BC，延长AC到点D，使得CD=CB，连接BD交⊙O于点E，过点E作BC的平行线交CD于点F．

（1）求证：AE=DE．

（2）求证：EF为⊙O的切线；

（3）若AB=5，BE=3，求弦AC的长．

知识回顾

垂径定理:垂直与弦的直径平分这条弦,并且平分这条弦所对的两段弧。

推论一:平分弦(不是直径)的直径垂直与这条弦,并且平分这条弦所对的两段弧。

推论二:弦的垂直平分线经过圆心，并且平分这条弦所对的弧。

推论三:平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧。

分析：（1）由图可知，要证明AE=DE，只要证明∠EAD=∠D即可．根据“同弧所对的圆周角相等”可以得到∠DBC=∠CAE，即可得出∠EAD=∠D.

（2）欲证明EF是⊙O的切线，只要证明OE⊥EF即可．由圆周角相等得出弧相等，再根据垂径定理得出垂直，即可解决问题.

（3）证明△ABE∽△DBA，利用相似三角形的性质求出AE，再进一步求出AD，即可解决问题．

请大家注意，想要正确解答一道数学题，必须先将大体思路弄清楚。下面，我们就按照以上思路来解答此题吧！

解答：（以下过程可以部分调整）

（1）证明：∵CD=CB，

∴∠DBC=∠D，

又∵∠DBC=∠CAE，（同弧所对的圆周角相等）

∴∠D=∠CAE，

∴AE=DE．

（2）证明：连接OE，

∵AB=BC，

∴∠BAC=∠ACB，

∵∠ACB=∠DBC+∠D=2∠DBC=2∠CAE，

∴∠BAC=2∠CAE，

∴∠CAE=∠BAE，

∴点E为弧BEC的中点，

∴OE⊥BC，

∵EF∥BC，

∴OE⊥EF，

∴EF为圆O的切线．

（3）解：在△ABE和△DBA中，

∵∠BAE=∠D，∠ABE=∠DBA，

∴△ABE∽△DBA，

∴AB/EB＝DB/AB＝DA/AE，

∴AB^2=BE×DB，

∵AB=5，BE=3，

∴BD＝25/3，

DE＝BD-BE

＝25/3-3

＝16/3，

∴AE＝DE＝16/3，

∵AB/EB＝DA/AE，

∴DA＝80/9，

∵CD=CB=AB=5，

∴AC＝DA×CD＝35/9．

（完毕）

这道题属于综合题，考查了切线的判定，圆周角定理，等腰三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是正确找出相似三角形，运用线段比例解决问题。温馨提示：朋友们如果有不明白之处或者有更好的解题方法，欢迎大家留言讨论。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小纳创作整理编辑！