散布密集度(散布精度是什么意思)

导语：射表上的公算偏差、散布密集界究竟指的是什么？

在翻阅射表时，我们能看到射表为了表现射击精度，会用公算偏差和散布密集界来表示。那么，我们要怎么看这个散布密集界和公算偏差呢？（注：本文比较烧脑，不想看过程可直接划到结尾看结论）

射弹散布的产生

在介绍这些东西之前，我们先来弄明白，什么是射弹散布，以及为什么会产生射弹散布？

假如同一个射手在晴朗无风的情况下，用同一武器发射同一批弹药对同一目标进行射击。理论上，所有的弹着点都会打到目标的同一个点上，但是，这是不可能的，哪怕把所有的影响因素都控制到最小，也会有一些弹头落在不同的位置上，这便是弹道散布。

那么，弹道散布的是如何产生的呢？产生的原因大概可以分为三类，让我们一条一条来剖析：

1. 初速不一样造成的。 初速不一样的原因可以归咎到枪弹上，发射药的重量、温度不一致，造成初速变化；弹头的重量存在偏差，同一发射药，弹头重量约大，初速越低。枪弹的一致性越好，散弹散布就会越小，这就是为什么在测试射弹散布时要尽可能采用同一批弹药的原因。

2. 发射角不一样造成的。 在射击过程中，由于射手在瞄准过程中存在倾斜、抵肩位置发生变化以及武器每次射击时的一致性不一致都会造成发射角产生偏差。

3. 外弹道受到影响。 在弹头飞行的过程中，若存在扰流之类的，那么弹头就会受到影响。从外，弹头也在外弹道中产生至关重要的影响，若重量、外形差别较大，那么散布也会变大。

射弹散布的规律

通过上面的分析，我们可以看到，射弹散布对于抛射式武器来说是不可避免的。那么，它们有什么规律吗？通过上图我们可以发现：在大量射弹形成的散布，它不是均匀的，散布的中间密集，外部稀疏，射弹在一个方向上的分布服从正太分布；并且，我们可以发现它的形状类似一个焦点在Y轴上的椭圆。

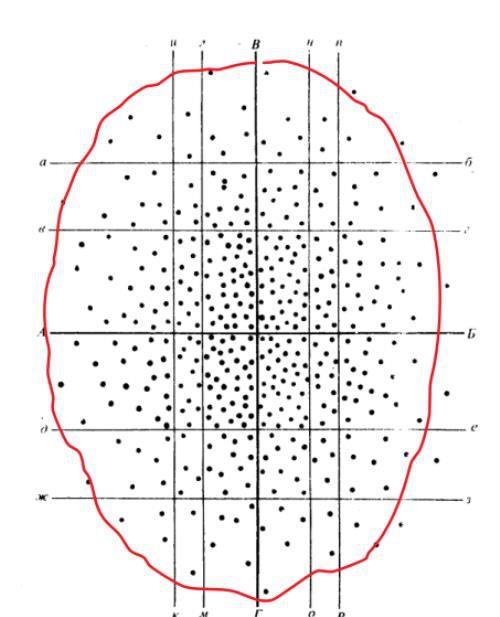
大量射弹产生的射弹散布

既然发现了规律，我们便可以用某种东西来概括它。首当其冲的是公算偏差。在介绍公算偏差之前，我们要先知道什么是平均弹着点。平均弹着点的求法有两种，一种是针对射弹量较多的。首先作一条水平的直线，要求这条直线上下两侧各分布有一半的射弹数目；再作一条竖直的直线与其垂直，要求这条直线左右两侧各分布有一半的射弹数目，这两条直线的交点即为平均弹着点。 其次为射弹数较少的时候，假设射弹数为4发，那么首先将任意两点连接，将其平分，接着中心点与剩余弹着点的任意一点连接，将这条线3等分，再将最后一个弹着点与该线上靠近前两发的点（注，若射弹数为3发，那么这个点便是这三发弹的平均弹着点）连接，将线4等分，靠近前三发的点便是这四发弹的平均弹着点。

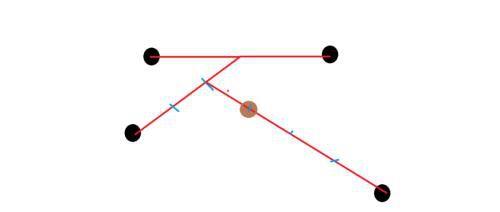
四发弹的平均弹着点求法

现在我们将一个方向上的散布以平均弹着点为中心，将散布面两边各平分四份得到一共8份的散布，那么每一段都是一个公算偏差。由于射弹散布是不均匀的，所以每个公算偏差里包含的射弹数是不同的，但总体的趋势是从中心到两边射弹数减小。从中心沿两边每一份公算偏差分别包含了射弹数的25%，16.1%，6.7%，1.8%。公算偏差包含了方向公算偏差和高低公算偏差。

高低公算偏差示意图，棕色的水平线经过平均弹着点，每两个相邻的蓝色包含一份公算偏差

前面说到，我们经过统计发现散布是满足正态分布的，那么我们就可以用标准差δ来形容散布。大量射击时，等于±δ的散布界包含了全部弹着的68.3%，那么这个散布区便称作散布密集界。我国为了简化计算，将一个散布密集界的射弹数取做70%。一个散布密集界包含了整个散布面的射弹数的30%，即一个散布面约等于3个散布密集界。通过散布密集界，我们也可以可以很容易求得一把武器的射弹面大小。

回到我们第一张散布图，有没有发现水平和高低方向上各被分成了3份，每一份就是一个散布密集界

在近距离射击上，垂直面上的散布可以近似原型，所以我们可以通过这个圆的半径来判定散布面的大小。以平均弹着点为中心画一个圆，若该圆包含了50%的射弹数，那么这个这个圆的半径便是R50，若这个圆包含了所有的射弹数，那么这个这个圆的半径便是R100。

这个R50、R100与散布密集界和公算偏差存在什么关系呢？以平均弹着点为中心画个正方形，这个正方形包含了50%的弹着点（注意了，是整个正方形包含的面积不是正方形的一条边包含了这个方向上的50%）。那么高低和方向上的散布界的长度分别是（0.5）^2=0.707，经过查命中公算的表得，含70.7%弹着点的散布界包括了对散布轴两边的偏差不大于1.56 个公算偏差的所有弹着点，所以这个正方形的长度为1.56 x 2 = 3.12个公算偏差，所以这个正方形的面积等于（3.12个公算偏差）^2，如果把整个正方形等价成半径为R50的圆，那么很容易得πx R50^2 = （3.12个公算偏差）^2 ，最终我们得出R50 =1.76个公算偏差，同时，我们也能轻易求出，在散布面等于8个公算偏差的情况下，R100=（4/1.76）R50 = 2.3 x R50。

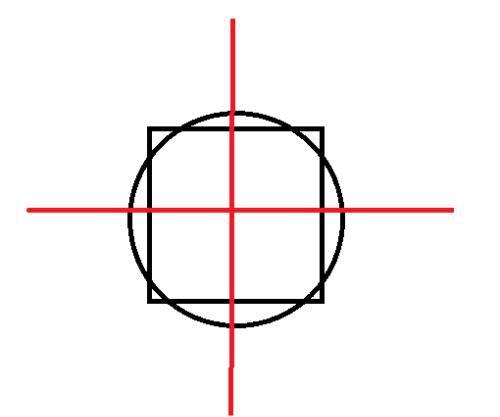
做个包含50%射弹散布的正方形和圆，圆的半径为1.76个公算偏差，正方形的宽为3.12个公算偏差，即包含了该方向上约70.7%的射弹数

R50与散布密集界的关系可以通过数学来表示。前面提过，散布满足正态分布，那么我们可以通过瑞利分布的概率密度函数来计算。已知概率密度函数为：

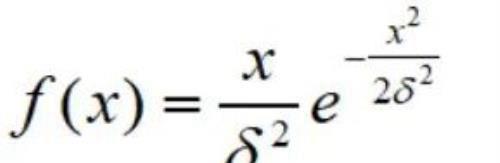
将其积分得到

已知射弹在R50圆内的概率为50%，可得F（R50）=0.5，R50 = δ（2ln2）^0.5 =1.177δ，R50/散布密集界 = 1.177/2 =0.57

散布面≈8公算偏差≈3散布密集界

R50=1.76 x（方向公算偏差 x高低方向偏差）^0.5 = 0.57散布密集界

R100 = 2.3 x R50

End

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小美创作整理编辑！