从代数和几何两个方面思考问题的区别(从代数和几何两个方面思考问题)

导语：从代数和几何两个方面思考问题

一道填空题，却难住了不少同学，下面让我们来见识一下它的风采：

已知线段AB=6，C、D是AB上的点，且AC=DB=1，P是线段CD上一动点，在AB的同侧分别作等边△APE和等边△PBF，G为线段EF的中点，点P由点C移动到点D时，G点移动的路径长度为__________

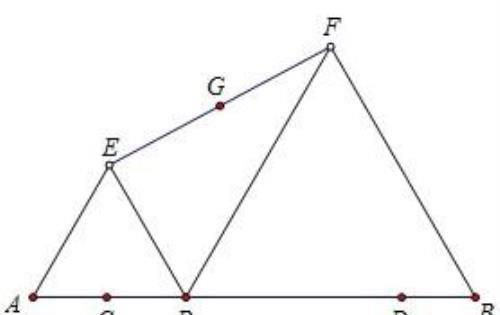
学生遇到的第一个难点是点G的运动路径是直线还是曲线，这个问题不弄清楚，后续解题无法进行；第二个难点才是点G的起始位置和终止位置。

先从几何角度来看这个问题：

由于题中的动点P带动了两个等边三角形的变化，而等边三角形的顶点E、F又决定了点G的位置，所以通过思考观察运动过程中两个等边三角形的变化，发现点E和点F始终在AE和BF的延长线上运动 ，不妨作AE和BF的延长线交于点H，如图所示

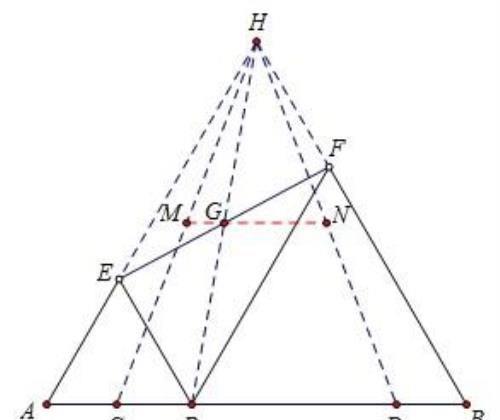
观察图中的四边形EPFH，可证其为平行四边形，EF是其对角线，连接PH，由平行四边形对角线互相平分可知点G即为其对角线交点，因为E、F在变化过程中，G点始终是其中点，所以可得到点G的路径其实是△HCD的中位线，如图中红色虚线MN，再由中位线定理计算出MN长度为2

再从代数角度来看这个问题：

抓住点G始终是线段EF的中点，若能建立平面直角坐标系，表示出点E、F的坐标，则可由中点公式求得G点坐标，只需要知道起点G1和终点G2的坐标即可。如图所示，E1、F1是当点P与点C重合时两个等边三角形的顶点位置，而E2、F2是当点P与点D重合时两个等边三角形的顶点位置。

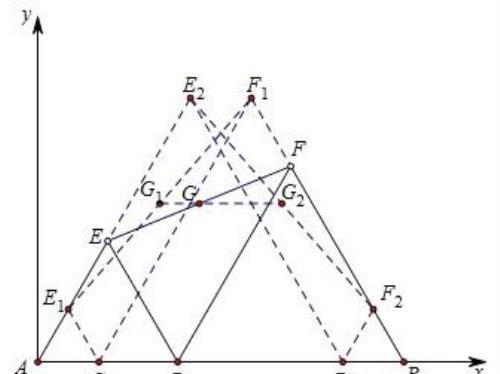
以点A为坐标原点，AB所在直线为横轴，其垂线为纵轴建立平面直角坐标系，可求得E1和F1坐标，同理求E2和F2坐标，由中点公式再求得G1和G2坐标即可得到线段G1G2的长度为2

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑！