如何表示这个方程的个根简单方程背后的公式(次方程有个根)

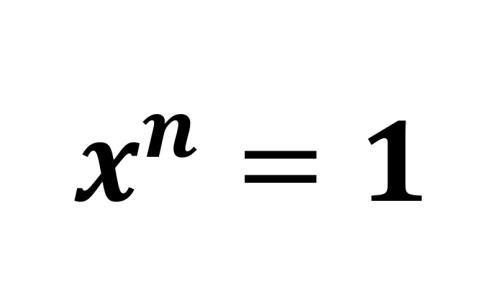
导语：如何表示这个方程的n个根？简单方程背后的高深数学

稍微懂点数学的同学可能知道n次多项式应该有n个根。即如下形式的多项式，

有n个解。让我们看一个简单的例子，

我们可以将其分解为，

这三个因子中至少有一个是零，因此x = -2， x = -1， x = 5就是这个三次多项式的根。另一种求这类多项式根的方法是画出它们的图形，并寻找图形与x轴相交的点，在上面的例子中，我们可以看到预期的三个这样的点，

然而，当我们看一个非常简单的n次多项式时，很难看出它怎么会有n个根，

以下是1≤n≤6时的多项式的图形，

可以看到，图中只显示了奇数次的一个根，以及偶数次的只有两个根（x =±1）。对于n = 1和n = 2，这很好，但对于n≥3，其他根在哪里？

复根和欧拉公式

这个难题的答案可以通过对多项式因式分解来找到，例如n=3的情况，

第一个因子告诉我们可以在图上看到的根（x=1），第二个因子（二次多项式）没有实根。这个二次方程的根是复数。因为这些根不是实数，所以它们不会出现在标准的实数x-y图中。

但是如果我们更仔细地观察复根的实部和虚部，会发现一些有趣的东西。实部的绝对值是1/2虚部的绝对值是

注意，1、根号3和2是角为π/3的直角三角形的边，因此cos(π/3) = 1/2，sin(π/3) =√3/2。因此这里的复根是

和

我们看到，所有三个根都可以由公式得到，

对应于k = 0，1，2。这对熟悉欧拉公式的人来说可能很熟悉，

由此我们可以得出这样的结论：

对于k = 0，1，2或者任何整数k因为这些值在复平面上绕半径为1的圆循环重复。根据这个观察，很容易将这个结果推广到任何形式的多项式：

它的根是

De Moivre定理另一种方法是使用De Moivre定理，

De Moivre定理很容易从上面的欧拉公式推导出来。现在如果我们用De Moivre定理，对于θ = 2kπ，有，

本文内容由小碧整理编辑！