组合构型(组合简单例题)

导语：组合构造第1章：容易求值2

【附】为便于有需要者编辑修改，特提供纯文本文档如下：

例3、求满足下列条件的最小正整数t，对于任何凸n边形A1A2…An，只要n≥t，就一定存在三点Ai、Aj、Ak（1≤i<j<k≤n），使△AiAjAk的面积不大于凸n边形A1A2…An面积的

（原创题）。

分析与解：当t=3、4、5时，从易于计算面积的角度考虑，可考察正三角形、正方形和正五边形，易知它们都不合乎条件，所以t≥6。

下面证明t=6合乎条件，即成立如下的命题。

当n≥6时，对任何凸边形A1A2…An，都存在1≤i<j<k≤n，使S≤，其中S为凸边形A1A2…An的面积。

再取特殊值研究。

当n=6时，问题变为：

引理：对任何凸六边形A1A2…A6，都存在1≤i<j<k≤6，使S≤，其中S为凸6边形A1A2…A6的面积。

证明：我们的目标是，要找到△AiAjAk，使S≤。这个要求包含2个部分：一是位置要求（顶点是原凸6边形的顶点）；二是数量要求，面积不大于。同时满足两个条件比较困难，可满足其中一个条件。注意到第一个条件是很容易满足的（任取3顶点即可），因此，可先满足第二个条件而弱化第一个条件：将3个顶点都是原顶点弱化为2个顶点是原顶点，而面积不大于。再调整，使3个顶点都是原顶点。

要找到一个三角形，使其面积不大于，由抽屉原理可以想到将凸6边形分割为6块，每一条边对应一块（2个原顶点），这是很容易办到的。在内部任取一个点P，连PAi（i=1，2，…，6）进行分割即可。

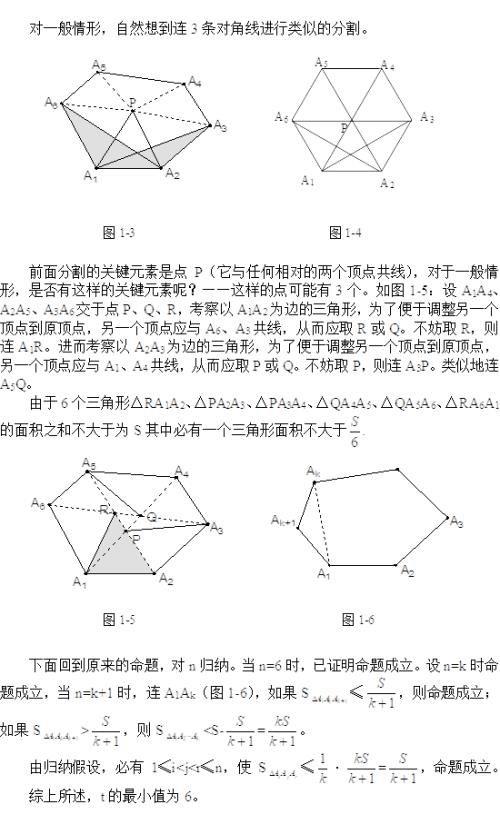
假定S≤，现在的问题是，如何将P替换成原顶点，而使面积不增加。这显然要找与A1A2距离最近的原顶点，它们是A6与A3。那么，A6与A3中是否有一个顶点合乎条件呢？考察三个三角形△A6A1A2、△PA1A2、△A3A1A2的面积关系，联想到一个熟悉的结论，知道当A6、P、A3共线时，问题已解决（图1-3）。由对称性，当A1、P、A4及 A2、P、A5都分别共线（因为△PA1A2是由抽屉原理找到的三角形）时问题已解决。于是，若3条对角线A1A3、A2A4、A3A6相交于一点P，则必存在△PAiAi+1，使≤（图1-4）。这样，由于Ai-1、P、Ai+2这3点共线，且P介于Ai-1、Ai+2之间，所以、中必有一个不大于。

前面分割的关键元素是点P（它与任何相对的两个顶点共线），对于一般情形，是否有这样的关键元素呢？——这样的点可能有3个。如图1-5：设A1A4、A2A5、A3A6交于点P、Q、R，考察以A1A2为边的三角形，为了便于调整另一个顶点到原顶点，另一个顶点应与A6、A3共线，从而应取R或Q。不妨取R，则连A1R。进而考察以A2A3为边的三角形，为了便于调整另一个顶点到原顶点，另一个顶点应与A1、A4共线，从而应取P或Q。不妨取P，则连A3P。类似地连A5Q。

由于6个三角形△RA1A2、△PA2A3、△PA3A4、△QA4A5、△QA5A6、△RA6A1的面积之和不大于为S其中必有一个三角形面积不大于

下面回到原来的命题，对n归纳。当n=6时，已证明命题成立。设n=k时命题成立，当n=k+1时，连A1Ak（图1-6），如果S≤，则命题成立；如果S>，则S<S-=。

由归纳假设，必有1≤i<j<r≤n，使S≤·=，命题成立。

综上所述，t的最小值为6。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小洁创作整理编辑！