导语：广东专插本高等数学第六章——考点集锦

【考纲要求】

掌握常数项级数的定义

常微分方程的定义：如给定一个数列{un},称u1+u2+u3+u4+⋯+un+⋯为（常数项）无穷级数，简称级数，记做从1到∞求和un。其中，u1+u2+u3+u4+⋯+un称作部分和Sn。

收敛的定义：部分和极限存在，则收敛；部分和极限不存在，则发散。

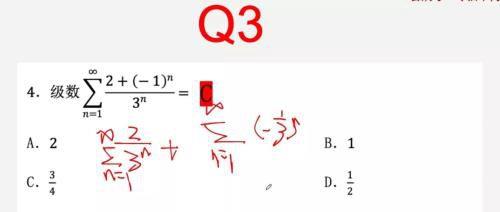
常见的常数项级数：1.等比级数 2. P级数 3. 调和级数

两个推论：1.若级数un和级数vn中一个收敛，一个发散，则级数un±vn一定发散；2.若 lim(n→∞)⁡un≠0,则级数un发散。

掌握常数项级数的比较审敛法

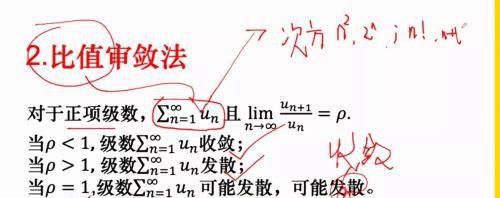
掌握常数项级数的比值审敛法

比较审敛法：首先需要注意，比较审敛法是针对两个级数的，是在两个级数之间进行比较的。结果为：大收小收，小发大发。收=收敛，发=发散。

比值审敛法：比值审敛法是针对一个级数的，求其后一项与前一项的比值。若比值小于1，则级数收敛；若比值大于1，则级数发散；若比值等于1，则无法判断敛散性。同时，注意比值审敛法比较适合求通项公式为次方、阶乘类型的级数。

放缩法思想：正弦和余弦的值小于等于1，利用该性质将愿级数放缩。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小故创作整理编辑！