初中数学几何一窍不通(数学题初中经典例题几何)

导语：初中数学，通过一道经典题目分享一下几何不等式的类型及相关定理

大家好，感谢你们的持续关注！今天继续为大家分享，今天给大家分享的内容是几何不等式的一些知识，不等式在数学中是一个比较大的知识点，而几何不等式也占了不少内容。另外它在我们实际生活中的应用也比较广泛，所以今天就给大家主要来分享几何不等式的类型以及几个定理。

平面图形中所含的线段长度、角的大小及图形的面积在许多情形下会呈现不等的关系。由于这些不等关系出现在几何问题中，所以就称之为几何不等式。这些问题难度较大，在解题中除了运用不等式的性质和已经证明过的不等式外，还需考虑几何图形的特点和性质。还是和以往一样我们先来看一道和几何不等式相关的题目：

如图，设BC是△ABC的最长边，在此三角形内部任选一点O，AO、BO、CO分别交对边于A′，B′，C′。证明：(1)OA′＋OB′＋OC′＜BC；(2)OA′＋OB′+OC′≤max｛AA′，BB′，CC′｝。

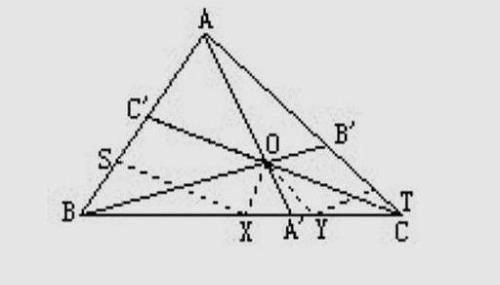
这道题难度稍大，我们分析下过点O作OX，OY分别平行于边AB，AC，交边BC于X，Y点，再过X，Y分别作XS，YT平行于CC′和BB′交AB，AC于S，T。由于△OXY∽△ABC，所以XY是△OXY的最大边，所以OA′＜max{OX，OY}≤XY．同理可求BX＞XS=OC′，CY＞OB′。下面看详细过程：

证明：（1）过点O作OX，OY分别平行于边AB，AC，交边BC于X，Y点，再过X，Y分别作XS，YT平行于CC′和BB′交AB，AC于S，T，由于△OXY∽△ABC，所以XY是△OXY的最大边，所以OA′＜max{OX，OY}≤XY，

又△BXS∽△BCC′，而BC是△BCC′中的最大边，从而BX也是△BXS中的最大边，而且SXOC′是平行四边形，

所以BX＞XS=OC′，

同理CY＞OB′，

所以OA′+OB′+OC′＜XY+BX+CY=BC，

（2）OA′/AA′=x，OB′/BB′=y，OC′/CC′=z

由于x+y+z=OA′/AA′+OB′/BB′+OC′/CC′=1

所以OA′+OB′+OC′=x•AA′+y•BB′+z•CC′，

≤（x+y+z）max{AA′，BB′，CC′}，

=max{AA′，BB′，CC′}。

这道题主要考查相似三角形的判定和性质以及作出适当的辅助线求解，关键是作OX，OY分别平行于边AB，AC，交边BC于X，Y点，再过X，Y分别作XS，YT平行于CC′和BB′交AB、AC于S、T。在解题过程中应用到了几何不等式。下面就把几何不等式的知识归纳一下：

几何不等式就其形式来说不外乎分为线段不等式、角不等式以及面积不等式三类，在解题中要用到一些有关的几何不等式的基本定理：

定理1 在三角形中，任两边之和大于第三边，任两边之差小于第三边。

定理2 同一个三角形中，大边对大角，小边对小角，反之亦然。

定理3 在两边对应相等的两个三角形中，第三边大的，所对的角也大，反之亦然。

定理4 三角形内任一点到两顶点距离之和，小于另一顶点到这两顶点距离之和。

好了有关几何不等式的知识已经给大家分享完了，如果对你有用可以点下关注，也可以收藏转发分享给其他的朋友，当然了也可以点赞，我在这里先谢谢啦！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小冰创作整理编辑！