高中数学求函数解析式的六种方法是什么(高中数学求函数解析式的六种方法总结)

导语：高中数学求函数解析式的六种方法

一、 待定系数法：

在已知函数解析式的构造时，可用待定系数法。

例题1、 设 f（x）是一次函数，且 f [ f（x）] = 4x + 3 ，求 f（x）的解析式。

解：设 f（x）= ax + b （a ≠ 0），则

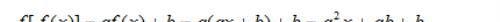
例题1图（1）

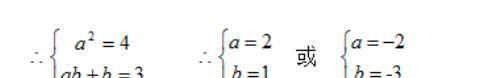
例题1图（2）

∴ f（x）= 2x + 1 或 f（x）= -2x - 3

二、 配凑法：

已知复合函数 f [ g（x）] 的表达式，求 f（x）的解析式， f [ g（x）] 的表达式容易配成 g（x）的运算形式时，常用配凑法。

但要注意所求函数 f（x）的定义域不是原复合函数的定义域，而是 g（x）的值域。

例题2、

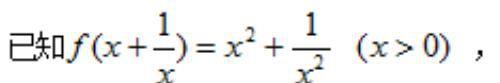
例题2图（1）

求 f（x）的解析式 。

解：

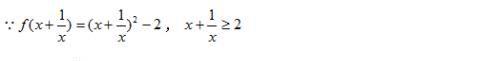
例题2图（2）

三、换元法：

已知复合函数 f [ g（x）] 的表达式时，还可以用换元法求 f（x）的解析式。

与配凑法一样，要注意所换元的定义域的变化。

例题3、已知

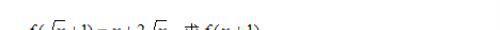
例题3图（1）

求 f（x + 1）的解析式 。

解：

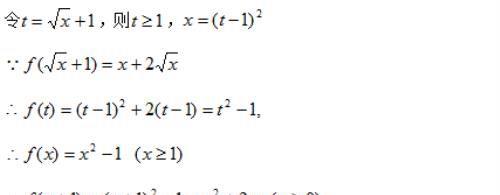
例题3图（2）

四、代入法：

求已知函数关于某点或者某条直线的对称函数时，一般用代入法。

例题4、已知：函数 y = x^2 + x 与 y = g（x）的图象关于点 （-2,3）对称，求 g（x）的解析式 。

解：

例题4图

五、构造方程组法：

若已知的函数关系较为抽象简约，则可以对变量进行置换，设法构造方程组，通过解方程组求得函数解析式。

例题5、

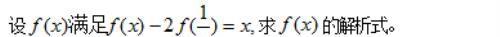
例题5图（1）

解：

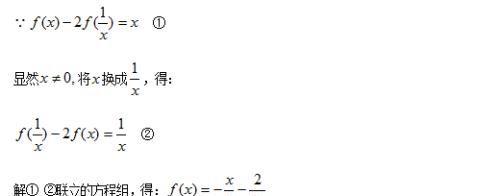
例题5图（2）

例题6、

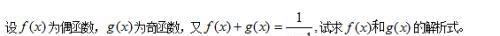
例题6图（1）

解：

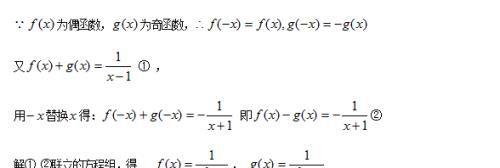
例题6图（2）

六、赋值法：

当题中所给变量较多，且含有“任意”等条件时，往往可以对具有“任意性”的变量进行赋值，使问题具体化、简单化，从而求得解析式。

例题7、

例题7图（1）

解：

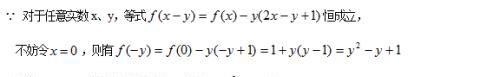
例题7图（2）

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小婷创作整理编辑！