“咬定青山不放松”(咬定青山不放松精神是什么意思)

导语：咬定青山不放松，盯紧参数便成功

咬定青山不放松，盯紧参数便成功

在二次函数压轴题中，含参数的解析式或方程，一直是学生解题的拦路虎，对代数恒等变换不熟练，或者信心不足，便会被淘汰掉。面对此类问题，首要任务便是克服对参数的恐惧，其次便是扎实的计算功底，第三就是细心与耐心。

题目

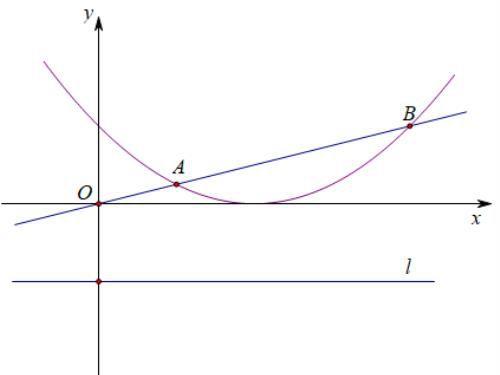
在平面直角坐标系xOy中，已知抛物线的顶点坐标为(2,0)，且经过点(4,1)，如图，直线y=1/4x与抛物线交于A、B两点，直线l为y=-1

(1)求抛物线的解析式；

(2)在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标，若不存在，请说明理由；

(3)已知F(s,t)为平面内一定点，M(m,n)为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标.

解析：

(1)在已知抛物线顶点的前提下，使用顶点式无疑最简单的，设y=a(x-2)²，将点(4,1)代入，求得a=1/4，于是y=1/4(x-2)²；

(2)熟悉将军饮马问题的学生，极容易找到方法，将点A或B中的一个点关于直线l的对称点作出，然后连接它与另一个点，与直线l的交点即为点P，如下图：

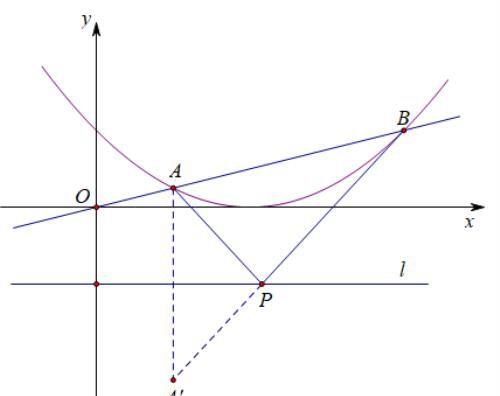
不妨作点A关于直线l的对称点A'(1,-9/4)，然后与点B(4,1)坐标一起，求出直线A'B的解析式为y=-13/12x+4/3，它与y=-1的交点即为点P(28/13,-1)；

(3)从条件中的描述我们知道，有两个距离相等，即点M到点F的距离和点M到直线l的距离，分别表示出来列出方程，这是一个较为复杂的含参数的方程，且参数较多，而在整理这个方程的过程中，牢记我们最终需要求什么，在整理之前，点M的坐标可写成(m,1/4(m-2)²)，这样在一开始便少掉一个参数n，消参和消元一样，而点F(s,t)为定点，意味着s和t均为常数，那么整个方程中，我们只重点关注m即可，因此整理的目标，就是一个含m的参数方程，如下图：

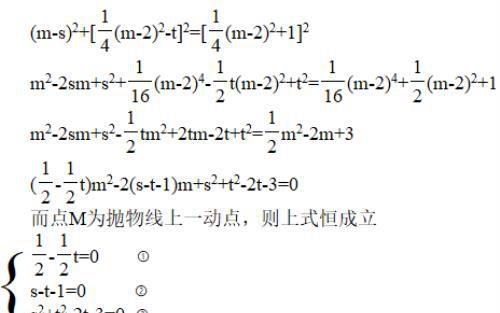
此问的理解难点就在于M为抛物线上一动点，换个说法，M为抛物线上任意一点，既然是任意一点，参数m可取任何实数，即对整理后的关于m的方程来讲，恒成立。

方程恒成立，初中阶段有一个最典型的模型就是Ax=B，其中A=0，B=0，而连小学生都知道“零乘任何数都为零”，即x为任何实数。

再分别解上述方程①，得t=1，代入到方程②得s=2，再到方程③中验证，左边=0，于是存在定点F(2,1)。

解题反思

等式恒成立，对初中阶段的学生来讲，理解上存在一定难度，而含参数的方程，任意实数均为它的根，意义与恒成立一样，即对于Ax=B这样的关于x的方程，系数A与常数项B均为零，此时x的值可取任意实数，都能使方程两边相等；拓展一下，若A=0，B≠0，则x取任意实数，方程两边均不相等。这个思路可用于解决函数恒过定点，以及恒不过定点的难题。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小岑创作整理编辑！