为什么有理数可数无理数不可数(为什么有理数是可数集)

导语：为什么有理数可数无理数不可数

有理数可数的证明：

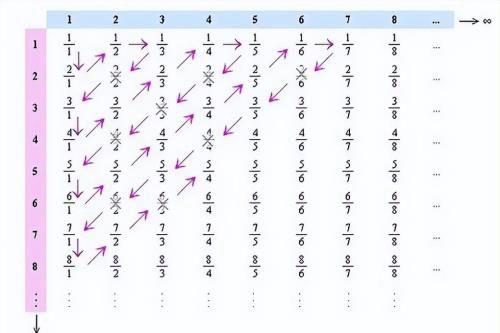
上面方法的证明思路就是，通过把所有的有理数都没有遗漏地一个个列出来（m/n中先m等于1，n变化，再m=2,n变化，。。。），并去除相同的数字，从而证明有理数确实是可以数出来的。

无理数不可数的证明：

如果无理数可数，则无理数能用正整数编号。

1 0.a11a12a13……

2 0.b11b12b13……

3 0.c11c12c13……

但是我们能找到一个无理数，这个数字十分位与a11的不同，百分位与b12的不同，千分位与c13的不同，等等。于是这个无理数与上面列出来的全不相等，也就是以上数列不可能包含所有的无理数。矛盾。因此无理数是不可数的。

这种方法并不能同样适用于证明有理数也不可数，因为无法保证找出来的那个数还是有理数。

从而有理数可数，无理数不可数，因此实数也不可数。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小故创作整理编辑！