高考解析几何运算技巧(解析几何占高考多少分)

导语：高考：解析几何这样算，学生直呼怎么不早教

中学解析几何是将几何图形置于直角坐标系中，用方程的观点来研究曲线，体现了用代数的方法解决几何问题的优越性，但有时运算量过大，或需繁杂的讨论，这些都会影响解题的速度，甚至会中止解题的过程，达到“望题兴叹”的地步。特别是高考过程中，在规定的时间内，保质保量完成解题的任务，计算能力是一个重要的方面。为此，从以下几个方面探索减轻运算量的方法和技巧，合理简化解题过程，优化思维过程。

技法一：巧用定义，揭示本质

定义是导出其性质的“发源地”，解题时，应善于运用圆锥曲线的定义，以数形结合思想为指导，把定量的分析有机结合起来，则可使解题计算量大为简化，使解题构筑在较高的水平上。

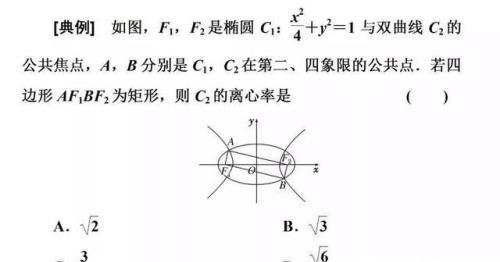
技法二：设而不求，整体代换

对于直线与圆锥曲线相交所产生的中点弦问题，涉及求中点弦所在直线的方程，或弦的中点的轨迹方程的问题时，常常可以用代点法求解。

方法点拨：本题设出A,B两点的坐标，却不需求出A,B两点的坐标，巧妙地表达出直线AB的斜率，通过将直线AB的斜率“算两次”建立几何量之间的关系，从而快速解决问题。

技法三：巧用“根与系数的关系”，化繁为简

某些涉及线段长度关系的问题可以通过解方程、求坐标，用距离公式计算长度的方法来解；但也可以利用一元二次方程，使相关的点的同名坐标为方程的根，由根与系数的关系求出两根间的关系或有关线段长度间的关系。后者往往计算量小，解题过程简捷。

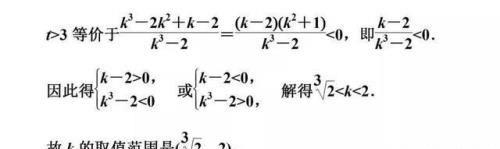
技法四：借“曲线系”，理清规律

利用曲线系解题，往往简捷明快，事半功倍，所以灵活运用曲线是解析几何中重要的解题方法和技巧之一。

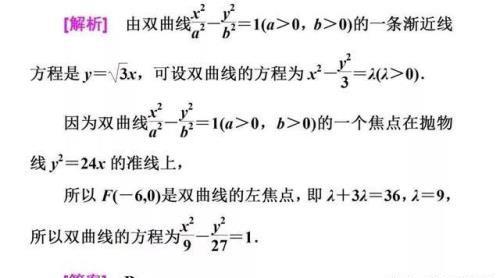
方法点拨：本题利用共渐近线系双曲线方程，可使问题马上得到解决。避免了复杂的判断、可能的分类讨论、繁杂的解方程组，事半功倍。

技法五：巧引参数，方便运算

换元引参是一种重要的数学方法，特别是解析几何中的最值问题、不等式问题等，利用换元引参使一些关系能够相互联系起来，激活了解题的方法，往往能化难为易，达到事半功倍。常见的参数可以选择点的坐标、直线的斜率、直线的倾斜角等。在换元过程中，还要注意代换的等价性，防止扩大或缩小原来变量的取值范围或改变原题条件。

方法点拨：求解本题利用椭圆的参数方程，可快速建立各点之间的联系，降低运算量。

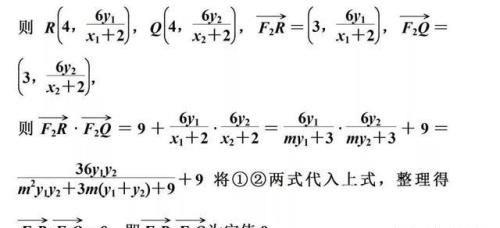
写在最后：解析几何的运算一直高中生学习数学畏惧的一块“难啃”的知识点，存在大多数的考生看到解析几何写完第一题就直接跳过的。本文通过五个运算技巧，简化解析几何的运算，希望能对广大师生有所帮助。

我是执笔学数学，欢迎各位留言，对本文进行批评指正。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小馨创作整理编辑！